Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 1cm + 2cm = 3cm < 4cm
⇒ bộ ba đoạn thẳng 1cm, 2cm, 4cm không thể tạo thành 1 tam giác.
b) 2cm + 3cm = 5cm.
⇒ Bộ ba đoạn thẳng 2cm; 3cm; 5cm không lập thành tam giác.
c) Ta có 3cm + 4cm = 7cm > 5cm.
Do đó bộ đoạn thẳng 3cm, 4cm, 5cm có thể thành 3 cạnh của tam giác.
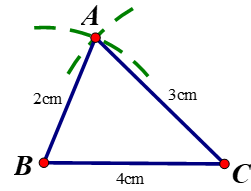
Cách dựng tam giác có ba độ dài 3cm, 4cm, 5cm :
- Vẽ BC = 4cm
- Dựng đường tròn tâm B bán kính 2cm ; đường tròn tâm C bán kính 3cm. Hai đường tròn cắt nhau tại A. Nối AB, AC ta được tam giác cần dựng.

Vì cạnh AB là cạnh lớn nhất nên góc C là góc lớn nhất. Chọn C

Bài 5. Cho bốn điển A, B, C, D không nằm trên đường thẳng a, trong đó A và B thuộc cùng một nửa mặt phẳng bờ a, còn C và D thuộc nửa mặt phẳng kia. Hỏi đường thẳng a cắt đoạn thẳng nào, không cắt đoạn thẳng nào trong các đoạn thẳng nối hai trong bốn điểm A, B, C, D?

Tự vẽ hình nha !
Xét tam giác đều ABC có :
\(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
Xét tam giác đều MDC có :
\(\widehat{DMC}=\widehat{MCD}=\widehat{CDM}=60^0\)
Ta có :
Góc ACB = ACM + MCB = 600
Góc MCD = MCB + BCD = 600
=> Góc ACM = Góc BCD
Xét tam giác ACM và tam giác BCD có :
AC = BC
CD = CM => tam giác ACM = tam giác BCD
Góc ACM = Góc BCD

3cm, 3cm, 5cm có thể là độ dài 3 cạnh của 1 tam giác
C đúng

Bài 1: (bạn tự vẽ hình vì hình cũng dễ)
Ta có: AB = AH + BH = 1 + 4 = 5 (cm)
Vì tam giác ABC cân tại B => BA = BC => BC = 5 (cm)
Xét tam giác BCH vuông tại H có:
\(HB^2+CH^2=BC^2\left(pytago\right)\)
\(4^2+CH^2=5^2\)
\(16+CH^2=25\)
\(\Rightarrow CH^2=25-16=9\)
\(\Rightarrow CH=\sqrt{9}=3\left(cm\right)\)
Tới đây xét tiếp pytago với tam giác ACH là ra AC nhé
Bài 2: Sử dụng pytago với tam giác ABH => AH
Sử dụng pytago với ACH => AC

Bộ ba độ dài nào sau đây có thể là độ dài 3 cạnh của một Tam giác:
A. 3cm;3cm;5cm. B. 2cm;3cm;5cm C.1cm;2cm;5cm D.1cm;2cm;3cm
Hok tốt.
Gọi cạnh còn lại có độ dài là x, theo bất đẳng thức tam giác ta có:
3 - 1 < x < 3 + 1 ⇒ 2 < x < 4 ⇒ x = 3. Chọn A