Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
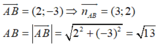
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
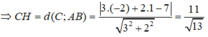
Diện tích tam giác ABC là:
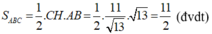
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
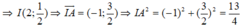
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
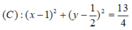

\(\overrightarrow{BA}=\left(2;4\right)\Rightarrow AB=\sqrt{2^2+4^2}=2\sqrt{5}\)
Gọi M là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}M\left(-1;0\right)\\AM=\dfrac{AB}{2}=\sqrt{5}\end{matrix}\right.\)
Đường tròn đường kính AB có tâm M và bán kính \(R=AM\) nên có pt:
\(\left(x+1\right)^2+y^2=5\)

\(\overrightarrow{AB}=\left(2,6\right)\)
\(\Rightarrow\overrightarrow{n}=\left(-6,2\right)\)
Đường thằng đi qua A(2,4) , nhận vecto \(\overrightarrow{n}\) làm vecto chỉ phương có PT :
\(\left(-6\right)\cdot\left(x-2\right)+2\cdot\left(y-4\right)=0\)
\(\Rightarrow-6x+2y+4=0\)

`|AB| = \sqrt((1-3)^2+(-2-4)^2)=2\sqrt10`
`=>` PT: `(x-1)^2+(y+2)^2=40`

Gọi M(2;1) và d lần lượt là trung điểm và đường trung trực của AB.
Một vectơ pháp tuyến của d là \(\overrightarrow{n}\)=\(\overrightarrow{AB}\)=(2;0).
Phương trình cần tìm:
d: 2.(x-2)+0.(y-1)=0 \(\Rightarrow\) x=2.

Gọi phương trình đường thẳng AB có dạng là \(y=ax+b\)
Ta có \(A\left(5;-2\right)\) và \(B\left(0;3\right)\) thuộc đt AB nên ta có hpt :
\(-2=5a+b\)
\(3=b\)
Ta tính được \(a=-1,b=3\)
Vậy phương trình đường thẳng AB có dạng \(y=-x+3\)
Trung điểm I của AB là: \(I\left(5;6\right)\)
Ta gọi pt đường thẳng AB có dạng: \(y=ax+b\)
\(\rightarrow\left\{{}\begin{matrix}5=a.4+b\\7=a.6+b\end{matrix}\right.\rightarrow\left\{{}\begin{matrix}a=1\\b=1\rightarrow\end{matrix}\right.AB:y=x+1\)
Gọi pt đường trung trực của AB là: \(y=ax+b\left(1\right)\)
Do (d) vuông góc với AB và d đi qua I nên:
\(\rightarrow\left\{{}\begin{matrix}a.1=-1\\6=a.4+b\end{matrix}\right.\)\(\rightarrow\left\{{}\begin{matrix}a=-1\\b=10\end{matrix}\right.\)\(\rightarrow\left(d\right):y=-x+10\)