Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

`a)`
`@ O(0;0), A(1;1), B(-1;1) in (P)`
`@ C(0;2), D(-2;0) in (d)`
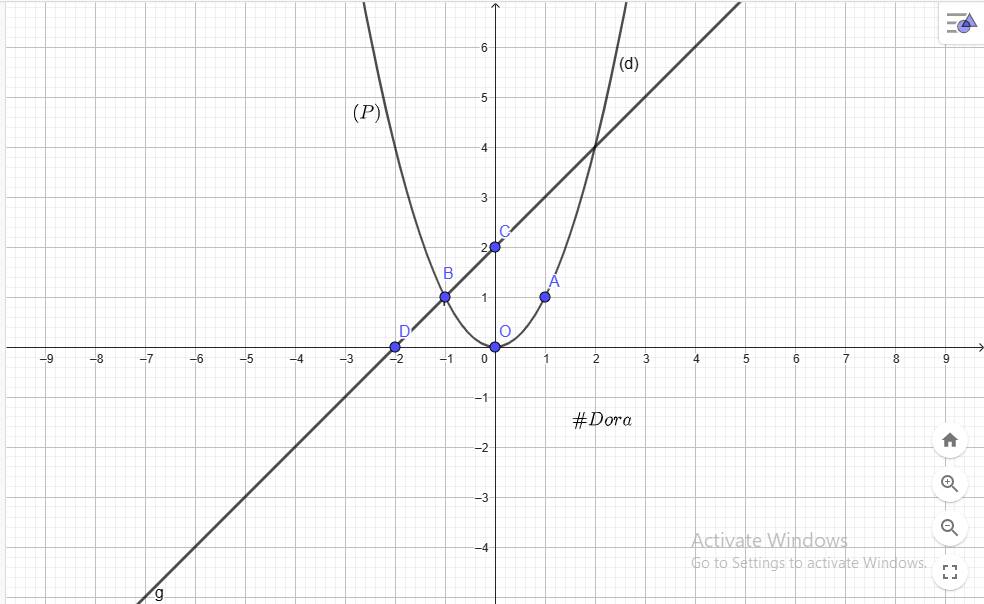
`b)` Ptr hoành độ của `(P)` và `(d)` là:
`x^2=x+2`
`<=>x^2-x-2=0`
Ptr có: `a-b+c=1+1-2=0`
`=>x_1=-1;x_2=-c/a=2`
`=>y_1=1;y_2=4`
`=>(-1;1), (2;4)` là giao điểm của `(P)` và `(d)`
`c)` Vì `(d') //// (d)=>a=1` và `b ne 2`
Thay `a=1;M(2;5)` vào `(d')` có:
`5=2+b<=>b=3` (t/m)
`=>` Ptr đường thẳng `(d'): y=x+3`

a) Vì A, B thuộc (P) nên:
x A = − 1 ⇒ y A = 1 2 ⋅ - 1 2 = 1 2 x B = 2 ⇒ y B = 1 2 ⋅ 2 2 = 2 ⇒ A − 1 ; 1 2 , B ( 2 ; 2 )
b) Gọi phương trình đường thẳng (d) là y = ax + b.
Ta có hệ phương trình:
− a + b = 1 2 2 a + b = 2 ⇔ 3 a = 3 2 2 a + b = 2 ⇔ a = 1 2 b = 1
Vậy (d): y = 1 2 x + 1 .
c) (d) cắt trục Oy tại điểm C(0; 1) và cắt trục Ox tại điểm D(– 2; 0)
=> OC = 1 và OD = 2
Gọi h là khoảng cách từ O tới (d).
Áp dụng hệ thức về cạnh và đường cao vào ∆ vuông OCD, ta có:
1 h 2 = 1 O C 2 + 1 O D 2 = 1 1 2 + 1 2 2 = 5 4 ⇒ h = 2 5 5
Vậy khoảng cách từ gốc O tới (d) là 2 5 5 .
a) Gọi đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=a'x+b'\)
Vì \(\left(d'\right)//\left(d\right)\Rightarrow a'=2\)
Vậy phương trình đường thẳng (d') có dạng \(\left(d'\right):y=2x+b'\)
Mặt khác (d') đi qua M(3;4) nên điểm M(3;4) thuộc \(\left(d'\right):y=2x+b'\)
Thay \(x=3;y=4\)vào hàm số \(y=2x+b'\)ta có:
\(4=2.3+b'\Leftrightarrow b'=-2\)
Vậy phương trình đường thẳng đi qua M(3;4) và song song với \(\left(d\right):y=2x+6\)là \(\left(d'\right):y=2x-2\)
b) Gọi OH là khoảng cách từ O đến (d). Gọi giao điểm của (d):y = 2x + 6 với hai trục Ox, Oy lần lượt là A(xA;0), B(0;yB).
Thay x = xA; y = 0 vào hàm số y = 2x + 6, ta có: \(0=2x_A+6\Leftrightarrow x_A=-3\)
Thay x = 0; y = yB vào hàm số y = 2x + 6, ta có: \(y_B=2.0+6=6\)
Vì \(OA=\left|x_A\right|;OB=\left|y_B\right|\)\(\Rightarrow OA=\left|-3\right|=3;OB=\left|6\right|=6\)
\(\Delta OAB\)vuông tại O, đường cao OH \(\Rightarrow\frac{1}{OH^2}=\frac{1}{OA^2}+\frac{1}{OB^2}\left(htl\right)\)
Rồi bạn thay OA, OB vào và dễ dàng tính được OH