Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1:
\(AB=\sqrt{\left[3-\left(-2\right)\right]^2+\left(3-2\right)^2}=\sqrt{26}\)
\(BC=\sqrt{\left(2-3\right)^2+\left(-2-3\right)^2}=\sqrt{26}\)
\(AC=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-2-2\right)^2}=4\sqrt{2}\)
\(P=\dfrac{AB+BC+AC}{2}=\dfrac{2\sqrt{26}+4\sqrt{2}}{2}=\sqrt{26}+2\sqrt{2}\)
\(S=\sqrt{\left(\sqrt{26}+2\sqrt{2}\right)\cdot2\sqrt{2}\cdot2\sqrt{2}\cdot\left(\sqrt{26}-2\sqrt{2}\right)}=\sqrt{18\cdot8}=12\left(đvdt\right)\)

Đáp án B

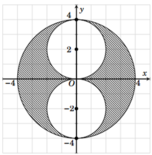
V 1 bằng thể tích khối trụ có bán kính đáy bằng 4 và chiều cao bằng 8 trừ bốn lần thể tích của vật tròn xoay tạo thành khi vật thể giới hạn bởi các đường x = 2 y , x = 0 , y = 0 , x = 4 quay quanh trục Oy
. V 1 = π .4 2 .8 − 4 π ∫ 0 4 2 y d y = 64 π . Thể tích
V 2 = 4 3 π ( 4 3 − 2 3 − 2 3 ) = 64 π .



làm đc chưa bạn...
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N
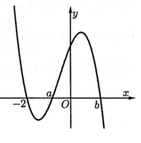

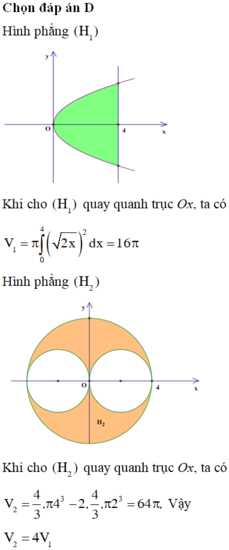
Chọn đáp án A
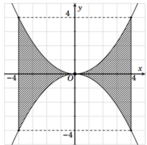
Hình phẳng H 1 được biểu diễn bằng miền tô đậm trong hình vẽ bên.
Thể tích khối trụ bán kính r = 4 chiều cao h = 8 là V = πr 2 h = 128 π đvtt
Thể tích của khối tròn xoay thu được khi quay hình phẳng giới hạn bởi parabol y = x 2 4 trục hoành, đường thẳng y = 4 xung quanh trục tung là
Suy ra thể tích của khối tròn xoay thu được khi quay H 1 quanh trục Oy là:
V 1 = V - 2 V P = 64 π (đvtt).
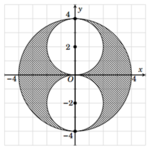
* Hình phẳng H 2 được biểu diễn bằng miền tô đậm trong hình vẽ bên.
Thể tích khối cầu lớn bán kính R = 4 là V L = 4 3 π . R 3 = 256 π 3 (đvtt)
Thể tích khối cầu nhỏ bán kính r = 2 là V N = 4 3 πr 3 = 32 π 3
Suy ra thể tích của khối tròn xoay thu được khi quay H 2 quanh trục Oy là