Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình đường thẳng qua điểm C là: 5x + 3y - 21 = 0
Tìm điểm D trên đường thẳng BC sao cho AD là đường cao của tam giác ABC.
Diện tích tam giác ABD là: \(S_{ABD} = \dfrac{1}{2} \cdot 1 \cdot \dfrac{2}{3} = \dfrac{1}{3}\)
Diện tích phần chứa điểm B là: \(S_{BCD} = \dfrac{1}{3}\)
Diện tích phần chứa điểm A là: \(S_{ACD} = S_{ABC} - S_{ABD} - S_{BCD} = \dfrac{1}{2} \cdot 1 \cdot \sqrt{26} - \dfrac{1}{3} - \dfrac{1}{3} = \dfrac{1}{2} \cdot \sqrt{26} - \dfrac{2}{3}\)
Vậy ta cần tìm điểm D sao cho AD là đường cao của tam giác ABC và \(S_{ACD} = 2S_{BCD}\)
Giải hệ phương trình tìm được D(2;4).
Vậy phương trình đường thẳng chia tam giác thành hai phần, phần chứa điểm A có diện tích gấp đôi phần chứa điểm B là: 5x - 3y - 7 = 0.

Gọi giao điểm của d và AB là D
\(\Rightarrow S_{ACD}=2S_{BCD}\)
\(\Rightarrow AD=2BD\Rightarrow\overrightarrow{AD}=\dfrac{2}{3}\overrightarrow{AB}\)
Gọi \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(2;-5\right)\\\overrightarrow{AD}=\left(x-1;y-4\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x-1=\dfrac{4}{3}\\y-4=-\dfrac{10}{3}\end{matrix}\right.\) \(\Rightarrow D\left(\dfrac{7}{3};\dfrac{2}{3}\right)\) \(\Rightarrow\overrightarrow{DC}=\left(\dfrac{11}{3};-\dfrac{8}{3}\right)=\dfrac{1}{3}\left(11;-8\right)\)
Đường thẳng d nhận \(\left(8;11\right)\) là 1 vtpt
Phương trình d:
\(8\left(x-6\right)+11\left(y+2\right)=0\Leftrightarrow8x+11y-26=0\)

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC
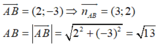
Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0
Kẻ CH ⊥ AB, (H ∈ AB)
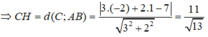
Diện tích tam giác ABC là:
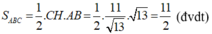
b) Viết phương trình đường tròn đường kính AB
Gọi I là trung điểm của AB
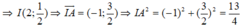
Đường tròn đường kính AB là đường tròn tâm I bán kính IA:
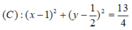

Viết PT đường trung tuyến BK
Xác định K:
xK = \(\frac{x_A+x_C}{2}\) = \(\frac{3}{2}\)
yK = \(\frac{y_A+y_C}{2}\) = \(\frac{9}{2}\)
(BK): \(\frac{x-x_B}{x_K-x_B}=\frac{y-y_B}{y_K-y_B}\)
=> (x-3)/(3/2 - 3) = (y+5)/(9/2 +5)
=> -2(x-3)/3 = 2(y+5)/19
=> -19x + 57 = 3y + 15
=> y = \(\frac{-19x}{3}+14\)
Đường thẳng (d1) vuông góc (BK) có dạng y = 3x/19 +c
do qua A(-1,2) => 2 = -3/19 + c => c = 2 + 3/19 = 41/19
=> (d1): y =\(\frac{3x}{19}+\frac{41}{19}\)
Giả sử đường thẳng cần tìm cắt BC tại M
Ta có \(\frac{S_{ABM}}{S_{ACM}}\)=2
mà S(ABM)/S(ACM) =(AH.BM/2)/(AH.CM/2) = \(\frac{BM}{CM}\) = 2 (AH là đường cao)
=> Vecto MB/ Vecto MC = -2
=> xM = (xB + 2xC)/ 3 = \(\frac{11}{3}\)
=> yM = (yB + 2yC)/3 = \(\frac{9}{3}\) = 3
=> Viết PT đường thẳng (d) đi qua A, M:
(x-xA)/(xM-xA)= (y-yA)/(yM-yA)
=> (x+1)/(11/3 +1) = (y-2)/(3-2)
4(x+1)/14 = y-2
=> y = \(\frac{2x}{7}+\frac{16}{7}\)