Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đặt w = x + yi , x ; y ∈ ℝ . Số phức w được biểu diễn bởi điểm M(x;y).
Ta có:
w = 3 + 4 i z + i = x + yi
⇔ z = x + y − 1 i 3 + 4 i = x + y − 1 i 3 − 4 i 25 = 3 x + 4 y − 4 + − 4 x + 3 y − 3 i 25
⇒ z = 1 25 3 x + 4 y − 4 2 + − 4 x + 3 y − 3 2 = 4
⇔ 3 x + 4 y − 4 2 + − 4 x + 3 y − 3 2 = 100 2
⇔ 3 x + 4 y 2 + − 4 x + 3 y 2 − 8 3 x + 4 y + 16 − 6 − 4 x + 3 y + 9 = 10000
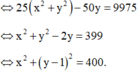
Vậy số phức w được biểu diễn bởi đường tròn tâm I(0;1), bán kính R = 20 và có phương trình: x 2 + y − 1 2 = 400 .

Đáp án A.
Gọi z = x ; y khi đó điều kiện trở thành:
x 2 + y − 1 2 = x 2 + y + 1 2 ⇔ y = − 1
Như vậy quỹ tích là một đường thẳng.





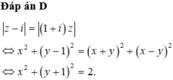
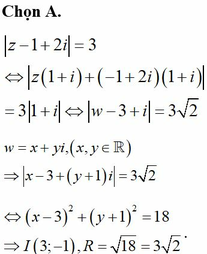
Đặt z = x + yi với x , y ∈ R
Từ giả thiết bài toán ta có
x + y i - 4 i + x + y i + 4 i = 10 ⇔ x + y - 4 i + x + y + 4 i = 10 ⇔ x 2 + y - 4 2 + x 2 + y + 4 2 = 10
Gọi F 1 0 ; - 4 , F 0 ; 4 . Khi đó M F 1 + M F 2 = 10
Vậy tập hợp các điểm M cần tìm là elip nhận F 1 F 2 = 8 làm tiêu cự, trục lớn bằng 10. Elip này có phương trình là x 2 9 + y 2 25 = 1
Đáp án B