Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8
Phép quay tâm O, góc , biến I thành I'(0;
), phép vị tự tâm O, tỉ số
biến I' thành I'' = (0;
.
) = (0;2). Từ đó suy ra phép đồng dạng có được bằng cách thực hiện liên tiếp phép quay tâm O, góc
và phép vị tự tâm O, tỉ số
biến đường tròn (I;2) thành đường tròn (I'';2
). Phương trình của đường tròn đó là
+
= 8

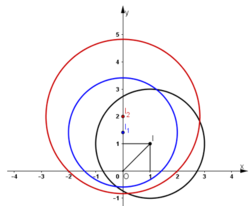
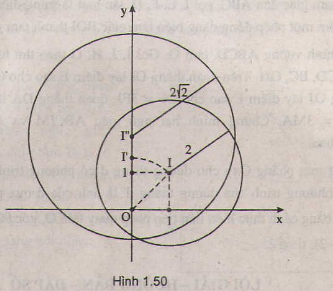
+ Gọi (I1; R1) = Q(O; 45º) (I; R) (Phép quay đường tròn tâm I, bán kính R qua tâm O một góc 45º).
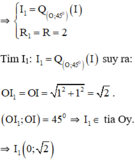
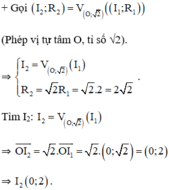
Vậy phương trình đường tròn cần tìm là (I2; R2): x2 + (y – 2)2 = 8.

Giả sử M 1 = D I ( M ) và M ′ = Q O ; − 90 ο ( M 1 ) . Ta có
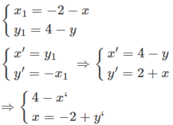
Thế (x;y) theo (x′;y′) vào phương trình d ta có:
3(y′ − 2) − (4 − x′) – 3 = 0 ⇔ x′ + 3y′ − 13 = 0
Vậy phương trình d’ là x + 3y – 13 = 0.

Dễ thấy bán kính của (C') = 4. Tâm I của (C') là ảnh của tâm I(1;2) của (C) qua phép đồng dạng nói trên. Qua phép vị tự tâm O tỉ số k = -2 , I biến thành I 1 ( − 2 ; − 4 ) . Qua phép đối xứng qua trục Ox, I 1 biến thành I′(−2;4).
Từ đó suy ra phương trình của (C') là x + 2 2 + y − 4 2 = 16 .







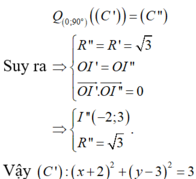
Gọi d 1 là ảnh của d qua phép vị tự tâm O tỉ số k = 0,5 thì phương trình của d 1 là x = 2 . Giả sử d' là ảnh của d qua phép quay tâm O góc 45 ο . Lấy M ( 2 ; 0 ) thuộc d 1 thì ảnh của nó qua phép quay tâm O góc 45 ο là M′(1;1) thuộc d'. Vì OM ⊥ d 1 nên OM′ ⊥ d′. Vậy d' là đường thẳng đi qua M' và vuông góc với OM'. Do đó nó có phương trình x + y – 2 = 0.