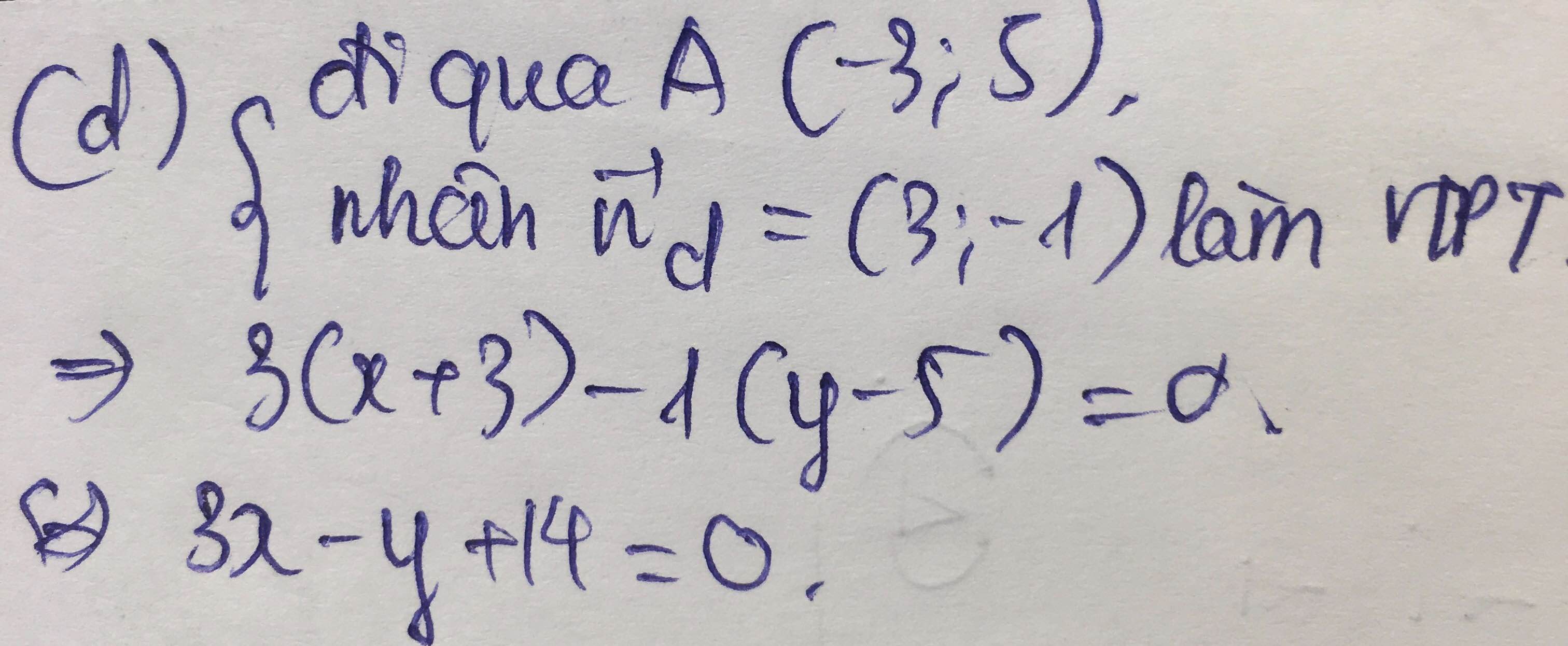
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
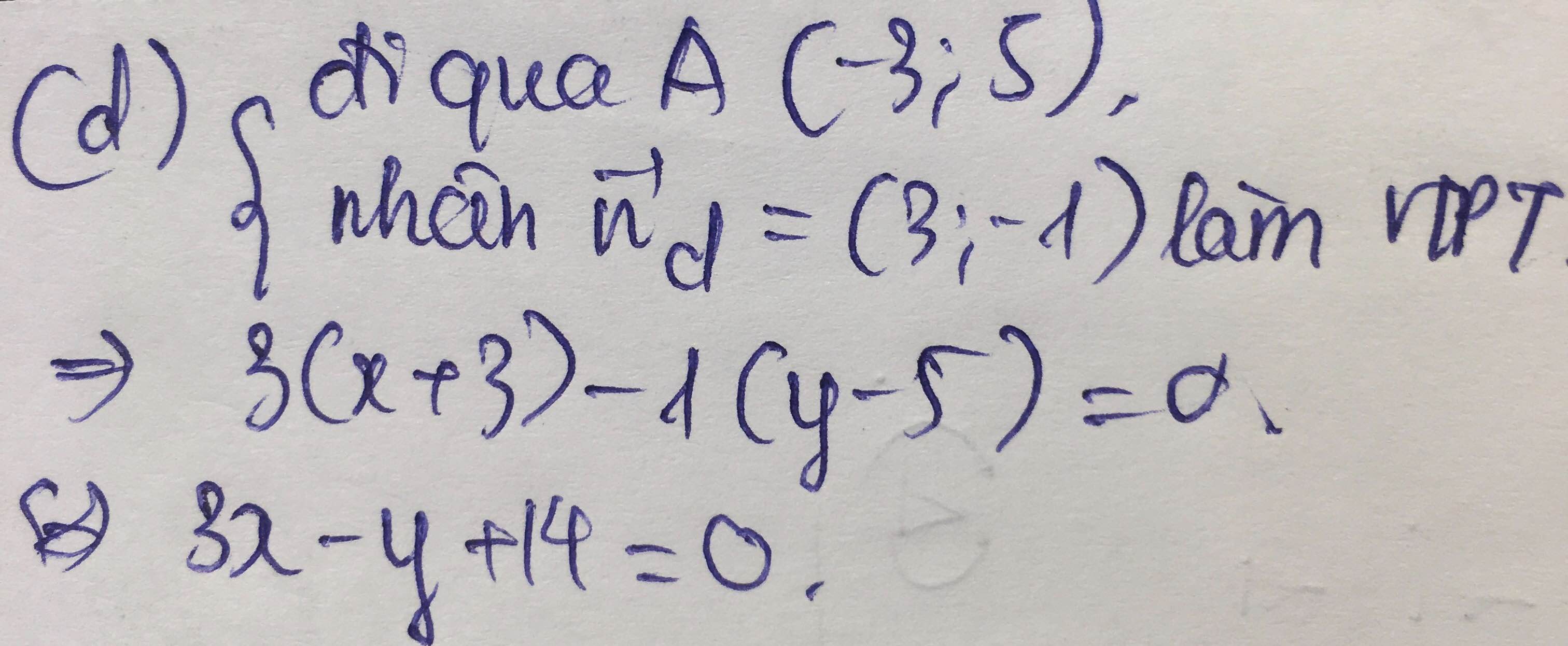
a: (Δ)//d nên Δ: -x+2y+c=0
=>VTPT là (-1;2)
=>VTCP là (2;1)
PTTS là:
x=3+2t và y=1+t
b: (d): -x+2y+1=0
=>Δ: 2x+y+c=0
Thay x=4 và y=-2 vào Δ, ta được:
c+8-2=0
=>c=-6
a) Khoảng cách từ điểm A đến đường thẳng \(\Delta \) là: \(d\left( {A,\Delta } \right) = \frac{{\left| {0 - 2 - 4} \right|}}{{\sqrt {{1^2} + {1^2}} }} = 3\sqrt 2 \).
b) Ta có: \(\overrightarrow {{n_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\). Phương trình đường thẳng a là:
\(1\left( {x + 1} \right) + 1\left( {y - 0} \right) = 0 \Leftrightarrow x + y + 1 = 0\)
c) Ta có: \(\overrightarrow {{u_a}} = \overrightarrow {{n_\Delta }} = \left( {1;1} \right)\).Từ đó suy ra \(\overrightarrow {{n_b}} = \left( {1; - 1} \right)\). Phương trình đường thẳng b là:
\(1\left( {x - 0} \right) - 1\left( {y - 3} \right) = 0 \Leftrightarrow x - y + 3 = 0\)
Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)
Denta tạo với d1, d2 1 tam giác cân với đỉnh là giao điểm của d1, d2 khi và chỉ khi denta vuông góc phân giác tạo bởi d1, d2
Gọi \(A\left(x;y\right)\) là 1 điểm bất kì thuộc phân giác tạo bởi 2 đường thẳng d1, d2
\(\Rightarrow\dfrac{\left|x-7y+17\right|}{\sqrt{1^2+\left(-7\right)^2}}=\dfrac{\left|x+y-5\right|}{\sqrt{1^2+1^2}}\Leftrightarrow\left|x-7y+17\right|=\left|5x+5y-25\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}5x+5y-25=x-7y+17\\5x+5y-25=-x+7y-17\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3y+\dfrac{21}{2}=0\\3x-y-4=0\end{matrix}\right.\)
\(\Rightarrow\Delta\) nhận \(\left(3;-1\right)\) hoặc \(\left(1;3\right)\) là 1 vtpt
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}3\left(x-0\right)-1\left(y-1\right)=0\\1\left(x-0\right)+3\left(y-1\right)=0\end{matrix}\right.\)
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
Gọi các đồ thị có CT chung là \(ax+b\)
\(a,\Leftrightarrow\left\{{}\begin{matrix}-a+b=-5\\a=0;b\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=0\\b=-5\end{matrix}\right.\Leftrightarrow\left(d_1\right):y=-5\\ b,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\a=2;b\ne-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=7\end{matrix}\right.\Leftrightarrow\left(d_2\right):y=2x+7\\ c,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\2a=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-2\\b=3\end{matrix}\right.\Leftrightarrow\left(d_3\right):y=-2x+3\\ d,\Leftrightarrow\left\{{}\begin{matrix}-a+b=5\\b=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-5\\b=0\end{matrix}\right.\Leftrightarrow\left(d_4\right):y=-5x\)
