Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có các vecto pháp tuyến: \(\overrightarrow{n_d}=\left(2;1\right);\overrightarrow{n_{d'}}=\left(1;3\right);\overrightarrow{n_{\Delta}}=\left(m;1\right)\)
a/ \(cos\left(d;d'\right)=\frac{\left|2.1+3.1\right|}{\sqrt{2^2+1^2}.\sqrt{1^2+3^2}}=\frac{\sqrt{2}}{2}\Rightarrow\left(d;d'\right)=45^0\)
b/ Để \(\Delta\) cùng tạo với d 1 góc 45 độ thì \(\Delta//d'\) hoặc \(\Delta\perp d'\)
\(\Rightarrow\left[{}\begin{matrix}\frac{m}{1}=\frac{1}{3}\\1.m+3.1=0\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=\frac{1}{3}\\m=-3\end{matrix}\right.\)
a: vecto AB=(6;-4)
PTTS là:
x=-6+6t và y=3-4t
b: Vì (d) vuông góc AB nên (d) có VTPT là (3;-2)
Phương trình(d) là:
3(x-3)+(-2)(y-2)=0
=>3x-9-2y+4=0
=>3x-2y-5=0
và song song với mặt phẳng (P): 2x - 3y + z - 2 = 0.
Đáp án B
Từ giả thiết suy ra
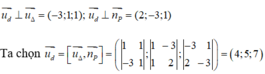
Mặt khác đường thẳng d đi qua điểm M(2;-1;1) nên phương trình tham số của đường thẳng d là: x = 2+ 4t, y = -1, + 5t, z = 1 + 7t.
Vậy đáp án đúng là B.
Gọi đường thẳng đi qua A là d'.
a) Ta có: \(d'\perp d.\)
\(\Rightarrow\) VTPT của d là VTCP của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\overrightarrow{u_{d'}}=\left(3;-4\right).\Rightarrow\overrightarrow{n_{d'}}=\left(4;3\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(4\left(x-2\right)+3\left(y+1\right)=0.\\ \Leftrightarrow4x+3y-5=0.\)
b) Ta có: \(d'//d.\)
\(\Rightarrow\) VTPT của d là VTPT của d'.
Mà VTPT của d là: \(\overrightarrow{n_d}=\left(3;-4\right).\)
\(\Rightarrow\) \(\overrightarrow{n_{d'}}=\left(3;-4\right).\)
\(\Rightarrow\) Phương trình đường thẳng d' là:
\(3\left(x-2\right)-4\left(y+1\right)=0.\\ \Leftrightarrow3x-4y-10=0.\)
a: Vì (d)//x-4y+5=0 nên (d): x-4y+c=0
Thay x=1 và y=0 vào (d), ta được:
c+1=0
=>c=-1
=>x-4y-1=0
b: Vì (d) vuông góc x-4y+5=0
nên (d): 4x+y+c=0
Thay x=1 và y=0 vào (d), ta được:
c+4=0
=>c=-4
=>4x+y-4=0
Gọi \(\overrightarrow{n}=\left(a;b\right)\) là 1 vtpt của đường thẳng d' cần tìm
Do d' tạo với d 1 góc bằng 45 độ
\(\Rightarrow cos\left(d;d'\right)=\dfrac{\left|2a+3b\right|}{\sqrt{2^2+3^2}.\sqrt{a^2+b^2}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\sqrt{2}\left|2a+3b\right|=\sqrt{13\left(a^2+b^2\right)}\)
\(\Leftrightarrow2\left(2a+3b\right)^2=13\left(a^2+b^2\right)\)
\(\Leftrightarrow5a^2-5b^2-24ab=0\)
\(\Rightarrow\left[{}\begin{matrix}a=5b\\b=-5a\end{matrix}\right.\) \(\Rightarrow\) chọn \(\left[{}\begin{matrix}\left(a;b\right)=\left(5;1\right)\\\left(a;b\right)=\left(1;-5\right)\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn:
\(\left[{}\begin{matrix}5\left(x-3\right)+1\left(y-6\right)=0\\1\left(x-3\right)-5\left(y-6\right)=0\end{matrix}\right.\) \(\Leftrightarrow...\)