Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}=\left(4;0\right)\)
\(\overrightarrow{AC}=\left(3;3\right)\)
\(\cos\widehat{A}=\dfrac{4\cdot3+3\cdot0}{\sqrt{4^2}+\sqrt{3^2+3^2}}=\dfrac{12}{4+3\sqrt{2}}=-24+18\sqrt{2}\)
=>Đề sai rồi bạn
Trong mặt phẳng oxy cho 2 điểm A(2;4), B(1;1) tìm tọa độ điểm C sao cho tam giác ABC vuông cân tại B

Giả sử \(C\) cần tìm có tọa độ là \(\left(x;y\right)\). Để tam giác ABC vuông cân tại B ta phải có:
\(\left\{{}\begin{matrix}\overrightarrow{BA}.\overrightarrow{BC}=0\\\left|\overrightarrow{BA}\right|=\left|\overrightarrow{BC}\right|\end{matrix}\right.\) với \(\overrightarrow{BA}=\left(1;3\right)\) và \(\overrightarrow{BC}=\left(x-1;y-1\right)\)
Điều đó có nghĩa là:
\(\left\{{}\begin{matrix}1.\left(x-1\right)+3\left(y-1\right)=0\\1^2+3^2=\left(x-1\right)^2+\left(y-1\right)^2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=4-3y\\\left(3-3y\right)^2+\left(y-1\right)^2=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=4-3y\\10y^2-20y=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=2\end{matrix}\right.\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}C\left(4;0\right)\\C\left(-2;2\right)\end{matrix}\right.\)

vecto AB=(-3;3)=(-1;1)
=>VTPT là (1;1)
Phương trình AB là: 1(x-1)+1(y-1)=0
=>x+y-2=0
vecto AC=(7;1)
=>VTPT là (-1;7)
Phương trình AC là
-1(x-1)+7(y-1)=0
=>-x+1+7y-7=0
=>-x+7y-6=0
=>x-7y+6=0
AB: x+y-2=0
AC: x-7y+6=0
Phương trình phân giác góc ngoài và góc trong của góc A sẽ là:
\(\dfrac{x+y-2}{\sqrt{2}}=\pm\dfrac{x-7y+6}{5\sqrt{2}}\)
=>\(\dfrac{x+y-2}{1}=\pm\dfrac{x-7y+6}{5}\)
=>5(x+y-2)=x-7y+6 hoặc -5(x+y-2)=x-7y+6
=>5x+5y-10-x+7y-6=0 hoặc -5x-5y+10-x+7y-6=0
=>4x+12y-16=0 hoặc -6x+12y+4=0
=>x+3y-4=0(d1) hoặc 3x-6y-2=0(d2)
Thay tọa độ B,C vào (d1), ta được:
t1=(-2)+3*4-4=-6+12=6 và t2=8+3*2-4=8+2=10
Thay tọa độ B,C vào (d2), ta được:
t3=3*(-2)-6*4-2=-6-2-24=-32 và t4=3*8-6*2-2=24-2-12=10
Vì t3*t4<0
nên (d2) chính là đường phân giác góc trong
=>(d2): 3x-6y-2=0
Tọa độ M là trung điểm của BC là:
x=(-2+8)/2=6/2=3 và y=(4+2)/2=3
vecto BC=(10;-2)=(5;-1)
Phương trình trung trực của BC là:
5(x-3)+(-1)(y-3)=0
=>5x-15-y+3=0
=>5x-y-12=0
Tọa độ H là:
5x-y=12 và 3x-6y=2
=>x=70/27 và y=26/27

vecto AH=(x+2;y-4); vecto BC=(-6;-2)
vecto BH=(x-4;y-1); vecto AC=(0;-5)
Theo đề, ta có: -6(x+2)-2(y-4)=0 và 0(x-4)-5(y-1)=0
=>y=1 và -6(x+2)=2(y-4)=2*(1-4)=-6
=>x+2=1 và y=1
=>x=-1 và y=1

Gọi \(C\left(x;y\right)\)
Khi đó : \(\overrightarrow{BA}=\left(1;3\right)\) , \(\overrightarrow{BC}=\left(x-1;y-1\right)\)
\(AB=\sqrt{\left(1-2\right)^2+\left(1-4\right)^2}=\sqrt{10}\)
\(BC=\sqrt{\left(x-1\right)^2+\left(y-1\right)^2}\)
Tam giác ABC vuông cân tại B khi \(\begin{cases}BA=BC\\\overrightarrow{BA}.\overrightarrow{BC}=0\end{cases}\)
\(\Rightarrow\begin{cases}\left(x-1\right)^2+\left(y-1\right)^2=10\\\left(x-1\right)+3\left(y-1\right)=0\end{cases}\)
Tới đây bạn tự giải được rồi :)
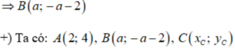

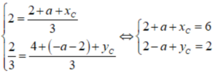
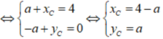
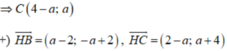
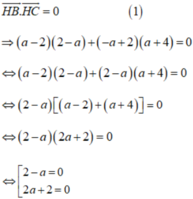
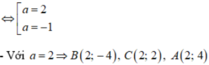
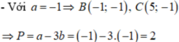




Theo công thức trọng tâm:
\(\left\{{}\begin{matrix}\frac{0+1+2m+1}{3}=2\\\frac{2+1+m+7}{3}=4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}2m+2=6\\m+10=12\end{matrix}\right.\) \(\Rightarrow m=2\)