Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I(a; b) là tâm đường tròn ngoại tiếp tam giác ABC.
A I 2 = B I 2 A I 2 = C I 2 ⇔ a − 0 2 + b − 2 2 = a + 2 2 + b − 8 2 a − 0 2 + b − 2 2 = a + 3 2 + b − 1 2
⇔ a 2 + b 2 − 4 b + 4 = a 2 + 4 a + 4 + b 2 − 16 b + 64 a 2 + b 2 − 4 b + 4 = a 2 + 6 a + 9 + b 2 − 2 b + 1
4 a − 12 b = − 64 6 a + 2 b = − 6 ⇔ a − 3 b = − 16 3 a + b = − 3
⇔ a = − 5 2 b = 9 2
Chọn B.

Gọi I(x, y). Ta có A I → = x + 4 ; y − 1 B I → = x − 2 ; y − 4 C I → = x − 2 ; y + 2 .
Do I là tâm đường tròn ngoại tiếp tam giác ABC nên:
I A = I B = I C ⇔ I A 2 = I B 2 I B 2 = I C 2
⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 x − 2 2 + y − 4 2 = x − 2 2 + y + 2 2 ⇔ x + 4 2 = x − 2 2 + 9 y = 1 ⇔ x = − 1 4 y = 1 .
Chọn B.

Gọi I( x; y). Ta có A I → = x + 4 ; y − 1 B I → = x − 2 ; y − 4 C I → = x − 2 ; y + 2 .
Do I là tâm đường tròn ngoại tiếp tam giác ABC nên I A = I B = I C ⇔ I A 2 = I B 2 I B 2 = I C 2
⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 x − 2 2 + y − 4 2 = x − 2 2 + y + 2 2 ⇔ x + 4 2 + y − 1 2 = x − 2 2 + y − 4 2 y − 4 2 = y + 2 2 ⇔ x + 4 2 = x − 2 2 + ( 1 − 4 ) 2 y = 1 ⇔ x 2 + 8 x + 16 = x 2 − 4 x + 4 + 9 y = 1 ⇔ x = − 1 4 y = 1 .
Chọn B.

Tham khảo!
Gợi ý: Gọi H là trực tâm tam giác ABC. Dễ dàng chứng minh được AD là phân giác góc EDF.
=> BD là phân giác góc FDG.
=> FG đối xứng với nhau qua BC.
=> BG vuông góc GC
Vẽ đường GC tìm được tọa độ của C
Vẽ đường BC.
Gọi I là giao điểm của FG và BC tìm tọa độ của I có I rồi tìm được tọa độ của F có F thì vẽ được đường thẳng AB.

B A D D C H K M I
Ta có \(HK\perp BC,K\in BC;\overrightarrow{HK}=\left(0;-2\right)\Rightarrow y-1=0\)
Gọi M là trung điểm của BC ta có phương trình \(x+3=0;M=IM\cap BC\Rightarrow M\left(-3;1\right)\)
Gọi D là điểm đối xứng của A qua I chỉ ra BHCD là hình bình hành. Khi đó M là trung điểm của HD, suy ra D(-5;-1).
I là trung điểm của AD, suy ra A(-1;7)
\(AI=\sqrt{20}\), phương trình đường tròn ngoại tiếp tam giác ABC là : \(\left(x+3\right)^2+\left(y-3\right)^2=20\)
Tọa độ điểm B, C là nghiệm của hệ phương trình :
\(\begin{cases}y-1=0\\\left(x+3\right)^2+\left(y-3\right)^2=20\end{cases}\)\(\Leftrightarrow\begin{cases}x=1\\y=1\end{cases}\) hoặc \(\begin{cases}x=-7\\y=1\end{cases}\)
Vậy ta có \(B\left(1;1\right),C\left(-7;1\right)\) hoặc \(B\left(-7;1\right),C\left(1;1\right)\)
Suy ra \(A\left(-1;7\right);B\left(1;1\right),C\left(-7;1\right)\)
hoặc\(A\left(-1;7\right);B\left(-7;1\right),C\left(1;1\right)\)

I nằm trên Δ nên I(x;2x+1)
\(IA=IB\)
=>IA^2=IB^2
=>(x+1)^2+(2x+1-1)^2=(x-1)^2+(2x+1+3)^2
=>x^2+2x+1+4x^2=x^2-2x+1+4x^2+16x+16
=>14x+17=2x+1
=>12x=-16
=>x=-4/3
=>I(-4/3;-5/3)
mà A(-1;1)
nên \(R=\sqrt{\left(-1+\dfrac{4}{3}\right)^2+\left(1+\dfrac{5}{3}\right)^2}=\dfrac{\sqrt{65}}{3}\)
=>\(\left(C\right):\left(x+\dfrac{4}{3}\right)^2+\left(y+\dfrac{5}{3}\right)^2=\dfrac{65}{9}\)
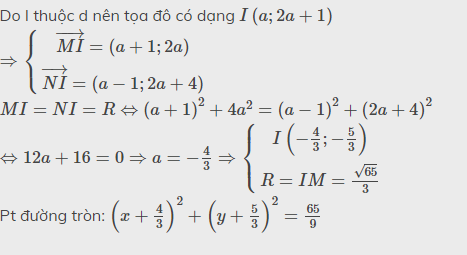
Ta thấy A,B một điểm thì thuộc trục tung, một điểm thì thuộc trục hoành nên tam giác OAB vuông tại O
=> Tâm đường tròn ngoại tiếp là trung điểm của AB
có tọa độ (2; -1)