K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

2 tháng 6 2022
Câu 1:
a: Vì I thuộc trục Ox nên I(x;0)
\(\overrightarrow{AI}=\left(x+1;-1\right)\)
\(\overrightarrow{AB}=\left(1;2\right)\)
Vì A,I,B thẳng hàng nên \(\dfrac{x+1}{1}=-\dfrac{1}{2}\)
=>x=-3/2
b: \(\overrightarrow{AM}=\left(m+5;2m\right)\)
Vì A,M,B thẳng hàng nên \(\dfrac{m+5}{1}=\dfrac{2m}{2}\)
=>m+5=m(vô lý)

AT
30 tháng 3 2017
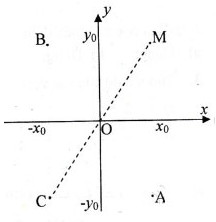
a) Hai điểm đối xứng nhau qua trục hoành thì có hoành độ bằng nhau và tung độ đối nhau.
M0 (x0; y0)=> A(x0;-y0)
b) Hai điểm đối xứng với nhau qua trục tung thì có tung độ bằng nhau còn hoành độ thì đối nhau.
M0 (x0; y0) => B(-x0;y0)
c) Hai điểm đối xứng nhau qua gốc O thì các tọa độ tương ứng đối nhau.
M0 (x0; y0) => C(-x0;-y0)


a: \(2\cdot\overrightarrow{AB}=\left(6;-16\right)\)
\(\overrightarrow{u}=2\cdot\overrightarrow{AB}-7\cdot\overrightarrow{i}\)
=(6-7;-16)=(-1;-16)
b: Gọi (d): y=ax+b là phương trình (AB)
Theo đề, ta có hệ:
-2a+b=5 và a+b=-3
=>a=-8/3; b=-1/3
=>(d): y=-8/3x-1/3
Khi y=0 thì -8/3x-1/3=0
=>-8/3x=1/3
=>x=-1/3:8/3=-1/3x3/8=-1/8
Vậy: Tọa độ giao điểm của (AB) với trục Ox là (-1/8;0)