Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tần số: \(f=\dfrac{1}{2\pi\sqrt {LC}}\Rightarrow f^2=\dfrac{a}{C}\) (a là 1 hằng số nào đó, do bài này f chỉ phụ thuộc vào C)
\(\Rightarrow f_1^2=\dfrac{a}{C_1}\)
\(f_2^2=\dfrac{a}{C_2}\)
Cần tìm: \(\Rightarrow f^2=\dfrac{a}{C}=a.(\dfrac{1}{C_1}+\dfrac{1}{C_2})=f_1^2+f_2^2\)
\(\Rightarrow f=\sqrt{30^2+40^2}=50(Hz)\)

Đáp án D
Phương pháp: Tính chu kì T
Cách giải: Cứ sau mỗi nửa chu kì thì q lại có độ lớn cực đại. Ta có:
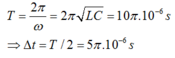

Điều kiện để xảy ra hiện tượng cộng hưởng và ULmax lần lượt là \(\begin{cases}Cộnghưởng\rightarrow Z_{L1}=Z_C\\U_{Lmax}\leftrightarrow Z_{L2}=\frac{R^2+Z^2_C}{Z_C}=Z_C+\frac{R^2}{Z_C}\end{cases}\)\(\rightarrow Z_{L1}<\)\(Z_{L2}\)
Điều này có nghĩa là khi đang cộng hưởng nếu tăng L thì sẽ tiến đến giá trị \(Z_{L2}\) nghĩa là \(U_L\) tăng dần đến giá trị cực đại.
Chọn D.

\(C = \frac{1}{\omega^2.L}= 5.10^{-6}F.\)
\(U_0 = \frac{q_0}{C}= \frac{I_0}{C.\omega}= \frac{I_0.\sqrt{L}}{\sqrt{C}} = 8V.\)
\(i = I = \frac{I_0}{\sqrt{2}}. \)
\(\left(\frac{u}{U_0}\right)^2+\left(\frac{i}{I_0}\right)^2=1\)
=> \(\left(\frac{u}{U_0}\right)^2 = 1- \left(\frac{i}{I_0}\right)^2 = 1 - \frac{1}{2}= \frac{1}{2}\)
=> \(u = \frac{1}{\sqrt{2}}U_0= 4\sqrt{2}V.\)

\(1=LC\omega^2=LC4\pi^2f^2\)
\(C=\frac{1}{L4\pi^2f^2}=\frac{8.10^{-6}}{\pi}F\)
\(\rightarrow A\)

Tần số của mạch LC lí tưởng f = 1 2 π LC → giảm C lên 4 lần và tăng L 9 lần thì f giảm 1,5 lần
Đáp án B

mình bị nhầm ở đáp án
A. \(\frac{4}{3}\mu s\) các câu khác cũng như vậy nhé
Năng lượng của mạch dao động W = \(\frac{Q_0^2}{2C}=\frac{LI^2_0}{2}\) → chu kì dao động của mạch
\(T=2\pi\sqrt{LC}=2\pi\frac{Q_0}{I_0}=16.10^{-6}\left(s\right)=16\mu s\).Thời gian điện tích giảm từ Q0 dến Q0/2
q = Q0cos \(\frac{2\pi}{T}t=\frac{Q_0}{2}\rightarrow\frac{2\pi}{T}t=\frac{\pi}{3}\rightarrow t=\frac{T}{6}=\frac{8}{3}\mu s\)
→ C

Đáp án C
Cách giải:
+ Ta có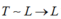
tăng 2 lần và C giảm 8 lần thì T giảm 2 lần.