Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Chọn C
Ta có h = d(I, (P)) = 1
Gọi (C) là đường tròn giao tuyến có bán kính r.
Vì S = r2.π = 2π <=> r = √2
Mà R2 = r2 + h2 = 3 => R = √3
Vậy phương trình mặt cầu tâm i (0; -2; 1) và bán kính R = √3
Khoảng cách từ A đến mặt phẳng (P) là :
\(h=d_{\left(A,\left(P\right)\right)}=\frac{\left|1.2+\left(-2\right).\left(-2\right)+2.1+5\right|}{\sqrt{1^2+\left(-2\right)^2+2^2}}=4\)
Gọi r là bán kính của đường tròn thiết diện thì ta có \(2\pi r=6\pi\Rightarrow r=3\)
Gọi R là bán kính mặt cầu cần tìm, ta có : \(R^2=h^2+r^2=4^2+3^2=25\)
Vậy phương trình mặt cầu cần tìm là : \(\left(x-1\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=25\)
Chọn C
(S) có tâm I (1; -2; 3) và bán kính R = 4
Gọi H là hình chiếu của I lên (P).
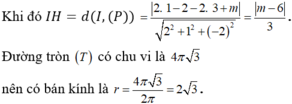
(P) cắt mặt cầu (S) theo giao tuyến là đường tròn (T) có chu vi bằng 4π√3
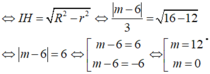
Vậy có 2 giá trị nguyên của m thỏa mãn.
Chọn D
Phương pháp
+ Cho mặt cầu (S) có tâm I và bán kính R và mặt phẳng (P) cắt mặt cầu theo giao tuyến là đường tròn có bán kính r thì ta có mối liên hệ 
với h = d(I,(P)). Từ đó ta tính được R.
Cách giải
+ Ta có
Đáp án D
Khoảng cách từ tâm I đến mặt phẳng (P) là d(I;(P))=3
Ta có R = r 2 + d 2 = 5 2 + 3 2 = 34 với R là bán kính mặt cầu (S)
Phương trình mặt cầu là S : x + 1 2 + y - 2 2 + z + 1 2 = 34
Đáp án B.
Phương pháp giải: Công thức tính bán kính đường tròn giao tuyến là
Lời giải:
Xét mặt cầu ( S ) : x - 1 2 + y - 2 2 + z - 2 2 = 9 có tâm I(1;2;2) bán kính R =3
Khoảng cách từ tâm I đến (P) là
Vậy bán kính đường tròn giao tuyến là
Đáp án B