K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 2 2021
\(\overrightarrow{AA'}=\left(0;0;3\right)=\overrightarrow{BB'}=\overrightarrow{CC'}\)
\(\Rightarrow\left\{{}\begin{matrix}B'\left(0;2;3\right)\\C'\left(-1;0;3\right)\end{matrix}\right.\)
\(\Rightarrow G\left(0;\dfrac{2}{3};3\right)\)

CM
8 tháng 5 2018
Đáp án B.
Cách 1: Ta có
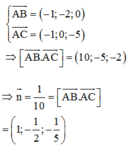
Cách 2:
Theo công thức phương trình đoạn chắn ta có phương trình
![]()
Suy ra phương trình pháp tuyến của (ABC) là
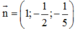

CM
9 tháng 11 2018
Đáp án B
Gọi I là trung điểm thỏa mãn
![]()
![]()
Khi đó
![]()
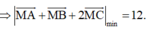
Dấu “=” xảy ra khi và chỉ khi
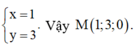

CM
18 tháng 7 2017
Đáp án C.
Vì OA = 1, OB = 2, OC = 3 và đôi một vuông góc
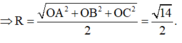
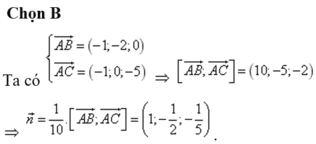
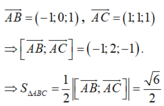

Giống bài trước \(\Rightarrow B'\left(0;2;3\right)\Rightarrow M\left(\dfrac{1}{2};1;\dfrac{3}{2}\right)\)