Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
![]()
lần lượt là VTPT của α ; β .
Gọi mặt phẳng cần tìm là mặt phẳng (P) có VTPT n p → .
Ta có:

Chọn C.

Đáp án C.
Phương pháp:
Mặt phẳng P : A x + B y + C z + D = 0 có 1 VTPT là n → = A ; B ; C .
Cách giải:
P : x − 4 y + 3 z − 2 = 0 có một vecto pháp tuyến là n 3 → = − 1 ; 4 ; − 3 .

Đáp án C.
Gọi I x ; y ; z thỏa mãn
I A → + 2 I B → + 5 I C → = 0 ⇒ x = 3 + 2. ( − 3 ) + 5. ( − 1 ) 8 = − 1 y = − 1 + 2.0 + 5. ( − 3 ) 8 = − 2 z = − 3 + 2. ( − 1 ) + 5.1 8 = 0
⇒ I = ( − 1 ; − 2 ; 0 )
Ta có
M A → + 2 M B → + 5 M C → = M I → + I A → + 2 M I → + 2 I B → + 5 M I → + 5 I C →
= 8 M I → + I A → + 2 I B → + 5 I C → = 8 M I →
⇒ M A → + 2 M B → + 5 M C → min ⇔ 8 M I → min <=> M là hình chiếu của I lên (P)
Gọi Δ là đường thẳng đi qua I − 1 ; 2 ; 0 và vuông góc với
( P ) : 2 x + 4 y + 3 z − 19 = 0 có vectơ chỉ phương là 2 ; 4 ; 3 ⇒ Δ : x = − 1 + 2 t y = − 2 + 4 t z = 3 t
Thế vào (P)
⇒ 2 ( − 1 + 2 t ) + 4 ( − 2 + 4 t ) + 3 ( 3 t ) − 19 ⇔ t = 1
⇒ x = 1 y = 2 z = 3 ⇒ M 1 ; 2 ; 3 ⇒ a + b + c = 6

Đáp án B
Phương pháp: (P)//(Q): x+2y+3z+2 = 0 => (P): x+2y+3z+m, m≠2
Thay tọa độ điểm A vào phương trình mặt phẳng (P) và tìm hằng số m
Cách giải:
(P)//(Q): x+2y+3z+2 = 0 => (P): x+2y+3z+m, m≠2
Mà ![]()
![]()
![]()

Ta có:
7/12 = 4/12 + 3/12 = 1/3 + 1/4 = 20/60 + 20/80
và 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 = (1/41 + 1/42 + 1/43 + ...+ 1/60) + (1/61 + 1/62 +...+ 1/79 + 1/80)
Do 1/41> 1/42 > 1/43 > ...>1/59 > 1/60
=> (1/41 + 1/42 + 1/43 + ...+ 1/60) > 1/60 + ...+ 1/60 = 20/60
và 1/61> 1/62> ... >1/79> 1/80
=> (1/61 + 1/62 +...+ 1/79 + 1/80) > 1/80 + ...+ 1/80 = 20/80
Vậy 1/41 + 1/42 + 1/43 +...+ 1/79 + 1/80 > 20/60 + 20/80 = 7/12

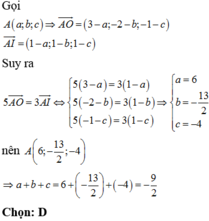
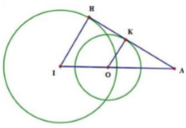

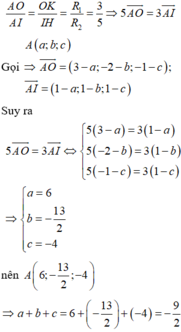

Đáp án C
P : x 2 + y 3 + z 4 = 1 ⇔ 6 x + 4 y + 3 z - 12 = 0