Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
Đường thẳng ∆ có vecto chỉ phương u ∆ → = 1 ; 1 ; - 1 .
Một mặt phẳng P có vecto pháp tuyến n p → = 1 ; 2 ; 3
Gọi I = ∆ ∩ P , tọa độ I là nghiệm của hệ phương trình:
x + 2 1 = y - 2 1 = z - 1 x + 2 y - 3 z + 4 = 0 ⇒ I - 3 ; 1 ; 1
Do d ⊂ P d ∩ ∆ ≢ ∅ ⇒ I ∈ d và d ⊂ P d ⊥ ∆
⇒ Đường thẳng d có một vecto chỉ phương u d → = u ∆ → , n P → = - 1 ; 2 ; 1
Vậy d : x + 3 - 1 = y - 1 2 = z - 1 1 .

Gọi H,I lần lượt là hình chiếu vuông góc của O lên (P) và ∆ .
Ta có d ( O; ∆ ) = OI ≥ OH. Dấu “=” xảy ra khi I = H.
Đường thẳng OH qua O ( 0;0;0 ) nhận n → = ( 1;2;1 ) làm vectơ chỉ phương nên có phương trình là x = t y = 2 t z = t
Mặt phẳng (P) có phương trình: x + 2y + z - 6 = 0.
Từ hai phương trình trên suy ra t = 1 nên H ( 1;2;1 ).
Khi đó (Q) là mặt phẳng chứa d và đi qua H.
Ta có M ( 1;1;2 ) ∈ d , vectơ chỉ phương của d là u → = ( 1;1;-2 ); H M → = ( 0;-1;1 ).
Suy ra vectơ pháp tuyến của (Q) là n → = n → ; H M → = ( -1;-1;-1 ) . Hơn nữa (Q) qua điểm M ( 1;1;2 ) nên (Q) có phương trình là:x + y + z - 4 = 0
Đáp án C


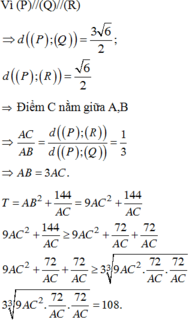


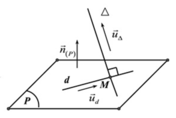


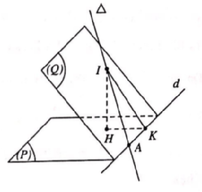


Đáp án B
Đường thẳng d có vecto chỉ phương u d → = 2 ; 1 ; 3 đi qua điểm M(1;0;-1)
Ta có n P → = u d → ; n Q → = - 4 ; 8 ; 0 mà (P) qua M ( 1 ; 0 ; - 1 ) ⇒ P : x - 2 y - 1 = 0 .