
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn A.
Gọi ∆ là đường thẳng cần tìm
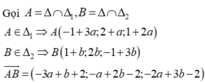
Đường thẳng d có vecto chỉ phương a d → = 0 ; 1 ; 1
![]()
![]()
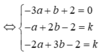
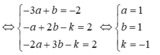
Ta có A(2;3;3); B(2;2;2)
∆ đi qua điểm A(2;3;3) và có vectơ chỉ phương ![]()
Vậy phương trình của ∆ là

B C A D H K J S
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)

Chọn A.
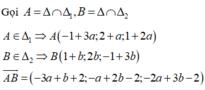
![]()

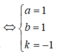
Ta có A(2;3;3); B(2;2;2)
Δ đi qua điểm A(2;3;3) và có vectơ chỉ phương A B → = 0 ; - 1 ; 1
Vậy phương trình của ∆ là x = 2 y = 3 - t z = 3 - t

Câu 28:
\(\overrightarrow{CB}=\left(1;-1;1\right)\)
Do (P) vuông góc BC nên nhận (1;-1;1) là 1 vtpt
Phương trình (P):
\(1\left(x-1\right)-1\left(y-1\right)+1\left(z+5\right)=0\)
\(\Leftrightarrow x-y+z+5=0\)
Câu 29:
Mạt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên nhận các vecto có dạng \(\left(k;-2k;3k\right)\) cũng là các vtpt với \(k\ne0\)
Do đó đáp án B đúng (ko tồn tại k thỏa mãn)
Với đáp án A thì \(k=-2\) , đáp án C thì \(k=3\), đáp án D có \(k=1\)

Đáp án B
Pt pháp tuyến của mặt phẳng cần tìm là n ⇀ = d , ⇀ ∆ ⇀ = (1;0;1)
Pt có dạng: x+z+D=0
Khoảng cách từ O (-1;1;-2) đến mp là 2
⇒ D=1
Pt có dạng : x+z+1=0

Đáp án C
Gọi C là trung điểm của AB ⇒ C(0;1;-1) ⇒ phương trình đường thẳng qua C và song song với AB là: x 1 = y - 1 - 1 = z + 1 2

\(\overrightarrow{u_{d1}}=\left(-1;1;1\right)\) ; \(\overrightarrow{u_{d2}}=\left(2;-1;-1\right)\)
\(\Rightarrow\left[\overrightarrow{u_{d1}};\overrightarrow{u_{d2}}\right]=\left(0;1;-1\right)\)
Do (P) song song \(d_1;d_2\Rightarrow\left(P\right)\) nhận \(\left(0;1;-1\right)\) là 1 vtpt
Phương trình (P) có dạng: \(y-z+c=0\)
Lấy \(A\left(2;0;0\right)\in d_1\) và \(B\left(0;1;2\right)\in d_2\)
Do (P) cách đều 2 đường thẳng \(\Rightarrow d\left(A;\left(P\right)\right)=d\left(B;\left(P\right)\right)\)
\(\Rightarrow\dfrac{\left|0-0+c\right|}{\sqrt{1^2+\left(-1\right)^2}}=\dfrac{\left|1-2+c\right|}{\sqrt{1^2+\left(-1\right)^2}}\Rightarrow\left|c\right|=\left|c-1\right|\)
\(\Rightarrow c=\dfrac{1}{2}\Rightarrow\) phương trình (P) có dạng:
\(y-z+\dfrac{1}{2}=0\)

Chọn D
Gọi vectơ pháp tuyến của mặt phẳng (P) là ![]() , a²+b²+c²>0.
, a²+b²+c²>0.
Phương trình mặt phẳng (P): a(x-4)+b (y-3)+c (z-4)=0.
Do (P) // Δ nên -3a+2b+2c=0 => 3a = 2 (b + c)
Mặt phẳng (P) tiếp xúc với (S) nên
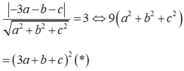
Thay 3a=2 (c+b ) vào (*) ta được:
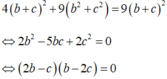
TH1: 2b-c=0, chọn b=1; c=2 => a = 2 => (P): 2x+y+2z-19=0 (thỏa).
TH2: b-2c=0, chọn c=1; b=2 => a = 2 => (P): 2x+2y+z-18=0 (loại do Δ ⊂ (P))
