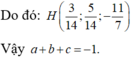Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lần sau em đăng bài ở học 24 để mọi người giúp đỡ em nhé!
Link đây: Cộng đồng học tập online | Học trực tuyến
1. Gọi I là tâm của mặt cầu cần tìm
Vì I thuộc d
=> I( a; -1; -a)
Mặt cầu tiếp xúc với hai mặt phẳng (p), (Q). nên ta co:
d(I; (P))=d(I;(Q))
<=> \(\frac{\left|a+2\left(-1\right)+2\left(-a\right)+3\right|}{\sqrt{1^2+2^2+2^2}}=\frac{\left|a+2\left(-1\right)+2\left(-a\right)+7\right|}{\sqrt{1^2+2^2+2^2}}\)
\(\Leftrightarrow\frac{\left|-a+1\right|}{3}=\frac{\left|-a+5\right|}{3}\Leftrightarrow a=3\)
=> I(3; -1; -3) ; bán kinh : R=d(I; P)=2/3
=> Phương trình mặt cầu:
\(\left(x-3\right)^2+\left(y+1\right)^2+\left(z+3\right)^2=\frac{4}{9}\)
đáp án C.
2. Gọi I là tâm mặt cầu: I(1; -1; 0)
Ta có: Phương trình mặt phẳng (P) tiếp xúc vs mặt Cầu S tại M
=> IM vuông góc vs mặt phẳng (P)
=> \(\overrightarrow{n_p}=\overrightarrow{MI}=\left(1;0;0\right)\)
=> Phương trình mặt phẳng (P) có véc tơ pháp tuyến: \(\overrightarrow{n_p}\)và qua điểm M
1(x-0)+0(y+1)+0(z-0) =0<=> x=0
đáp án B
3.
\(f\left(x\right)=\dfrac{1}{256}\left(2x+3\right)^{10}=\dfrac{1}{256} \sum \limits_{k=0} ^{10}C_{k}^{10}(2x)^k.3^{10-k}\)
Để có hệ số x^8 thì k=8 khi đó hệ số của x^8 là:
\(\dfrac{1}{256}C_{8}^{10}.2^8.3^{10-8}=405\)
đáp án D
4.
pt <=> \(\left(2.5\right)^{x^2-3}=10^{-2}.10^{3x-3}\)
\(\Leftrightarrow10^{x^2-3}=10^{3x-5}\)
\(\Leftrightarrow x^2-3=3x-5\Leftrightarrow x^2-3x+5=0\)
=> theo định lí viet tổng các nghiệm bằng 3, tích các nghiệm bằng 5
Đáp án A

Câu 28:
\(\overrightarrow{CB}=\left(1;-1;1\right)\)
Do (P) vuông góc BC nên nhận (1;-1;1) là 1 vtpt
Phương trình (P):
\(1\left(x-1\right)-1\left(y-1\right)+1\left(z+5\right)=0\)
\(\Leftrightarrow x-y+z+5=0\)
Câu 29:
Mạt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên nhận các vecto có dạng \(\left(k;-2k;3k\right)\) cũng là các vtpt với \(k\ne0\)
Do đó đáp án B đúng (ko tồn tại k thỏa mãn)
Với đáp án A thì \(k=-2\) , đáp án C thì \(k=3\), đáp án D có \(k=1\)

14.
Pt mp (P) qua A và vuông góc d:
\(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Gọi M là giao điểm d và (P) thì tọa độ M thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\) \(\Rightarrow M\left(2;5;1\right)\)
A' đối xứng A qua d \(\Rightarrow\)M là trung điểm AA'
Theo công thức trung điểm \(\Rightarrow A'\left(2;7;3\right)\)
15.
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=-2+3t\\y=-2+2t\\z=-t\end{matrix}\right.\)
PT (P) qua A và vuông góc d:
\(3\left(x-4\right)+2\left(y+3\right)-1\left(z-2\right)=0\)
\(\Leftrightarrow3x+2y-z-4=0\)
H là giao điểm d và (P) nên tọa độ thỏa mãn:
\(3\left(-2+3t\right)+2\left(-2+2t\right)+t-4=0\Rightarrow t=1\)
\(\Rightarrow H\left(1;0;-1\right)\)
11.
Thay tọa độ 4 điểm vào pt d chỉ có đáp án A thỏa mãn
12.
Phương trình (P) qua A và vuông góc \(\Delta\):
\(1\left(x-0\right)+1\left(y-1\right)-1\left(z+1\right)=0\Leftrightarrow x+y-z-2=0\)
Gọi M là giao điểm d và (P) thì tọa độ M thỏa mãn:
\(1+t+2+t-\left(13-t\right)-2=0\Rightarrow t=4\) \(\Rightarrow M\left(5;6;9\right)\)
\(\Rightarrow\overrightarrow{AM}=\left(5;5;10\right)=5\left(1;1;2\right)\)
Phương trình tham số d: \(\left\{{}\begin{matrix}x=t\\y=1+t\\z=-1+2t\end{matrix}\right.\) hoặc \(\left\{{}\begin{matrix}x=5+t\\y=6+t\\z=9+2t\end{matrix}\right.\)
13.
Pt tham số đường d qua A vuông góc (P): \(\left\{{}\begin{matrix}x=-t\\y=1-2t\\z=-2+2t\end{matrix}\right.\)
H là giao điểm (P) và d nên tọa độ thỏa mãn:
\(t-2\left(1-2t\right)+2\left(-2+2t\right)-3=0\Rightarrow t=1\)
\(\Rightarrow H\left(-1;-1;0\right)\)

14.
Mặt phẳng (P) nhận \(\overrightarrow{n}=\left(2;1;-2\right)\) là 1 vtpt
Đường thẳng d nhận \(\overrightarrow{u}=\left(1;-2;3\right)\) là 1 vtcp
Điểm \(M\left(2;0;-3\right)\) thuộc d nên cũng thuộc (Q)
(Q) vuông góc (P) và chứa d nên nhận \(\left[\overrightarrow{n};\overrightarrow{u}\right]=\left(1;8;5\right)\) là 1 vtpt
Phương trình (Q):
\(1\left(x-2\right)+8y+5\left(z+3\right)=0\)
\(\Leftrightarrow x+8y+5z+13=0\)
15.
Phương trình hoành độ giao điểm:
\(sinx=cosx\Rightarrow x=\frac{\pi}{4}\)
\(S=\int\limits^{\frac{\pi}{4}}_0\left(cosx-sinx\right)dx+\int\limits^{\pi}_{\frac{\pi}{4}}\left(sinx-cosx\right)dx=\sqrt{2}-1+\sqrt{2}+1=2\sqrt{2}\)
10.
Coi lại đề nào bạn, pt hình phẳng (D) có vấn đề, nhìn chữ -dx+4 kia ko biết phải nghĩ sao
11.
Cũng ko dịch được đề này, đoán đại: cho \(F\left(x\right)=x^2\) là 1 nguyên hàm của \(f\left(x\right).e^{2x}\). Tìm nguyên hàm của \(f'\left(x\right).e^{2x}\)
\(I=\int f'\left(x\right)e^{2x}dx\)
Đặt \(\left\{{}\begin{matrix}u=e^{2x}\\dv=f'\left(x\right)dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=2e^{2x}dx\\v=f\left(x\right)\end{matrix}\right.\)
\(\Rightarrow I=e^{2x}f\left(x\right)-2\int f\left(x\right)e^{2x}dx=e^{2x}f\left(x\right)-2x^2+C\)
12.
Đúng là \(y=\left(e+1\right)x\) và \(y=1+e^x\) chứ bạn? Hai đồ thị này cắt nhau tại 2 điểm, nhưng ko thể tìm được tọa độ của điểm thứ 2 đâu
13.
Hình chiếu của A lên Ox có tọa độ \(\left(1;0;0\right)\)

19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)

I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.

6.
Mặt phẳng Oxz có pt: \(y=0\)
Khoảng cách từ I đến Oxz: \(d\left(I;Oxz\right)=\left|y_I\right|=2\)
\(\Rightarrow R=2\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=4\)
7.
Mặt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên cũng nhận các vecto có dạng \(\left(k;-2k;3k\right)\) là vtpt
Bạn có ghi nhầm đề bài ko nhỉ? Thế này thì cả C và D đều ko phải vecto pháp tuyến của (Q)
4.
Đường thẳng d nhận \(\left(1;-2;2\right)\) là 1 vtcp
Gọi (P) là mặt phẳng qua M và vuông góc d \(\Rightarrow\) (P) nhận \(\left(1;-2;2\right)\) là 1 vtpt
Phương trình (P): \(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Tọa độ hình chiếu M' của M lên d là giao của d và (P) nên thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\)
\(\Rightarrow M'\left(2;5;1\right)\)
5.
(P) nhận \(\left(2;3;1\right)\) là 1 vtpt
Gọi d là đường thẳng qua I và vuông góc (P)
\(\Rightarrow\) d nhận \(\left(2;3;1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=-2+3t\\z=1+t\end{matrix}\right.\)
H là giao điểm của d và (P) nên tọa độ thỏa mãn:
\(2\left(1+2t\right)+3\left(-2+3t\right)+1+t-11=0\) \(\Rightarrow t=1\)
\(\Rightarrow H\left(3;1;2\right)\)