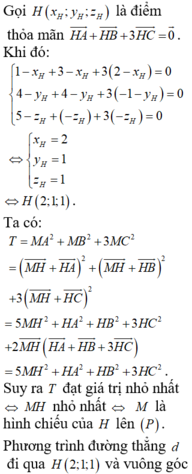Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
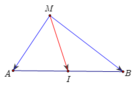
Gọi I, O lần lượt là trung điểm của AB và IC, khi đó với điểm M bất kỳ ta luôn có
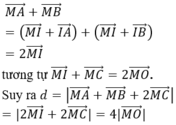
nên d nhỏ nhất khi và chỉ khi ![]() nên M là hình chiếu vuông góc của O lên (P). Có A(0; -2; -1), B (-2,-4,3) => I (-1 ; -3 ; 1), kết hợp với C (1; 3; -1) ta có O (0;0;0)
nên M là hình chiếu vuông góc của O lên (P). Có A(0; -2; -1), B (-2,-4,3) => I (-1 ; -3 ; 1), kết hợp với C (1; 3; -1) ta có O (0;0;0)
Đường thẳng qua O (0;0;0) vuông góc với (P) có phương trình 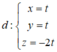
Giao điểm của d và (P) chính là hình chiếu vuông góc M của O (0;0;0) lên mặt phẳng (P).
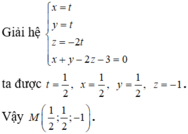

Đáp án C
Gọi G là trọng tâm của tam giác ABC => G(2;1;3)

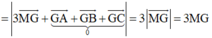
Suy ra MG min <=>M là hình chiếu của G trên (Oxy) => M(2;1;0)

Chọn D

Vậy M là hình chiếu vuông góc của G lên mặt phẳng (Oyz) nên M (0;1;4)

Đáp án D
Gọi I(a; b; c) thỏa mãn
![]()
Khi đó
![]()
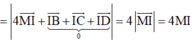
Suy ra MI min => M là hình chiếu của I trên (Oyz) => M(0;1;4)

Chọn B
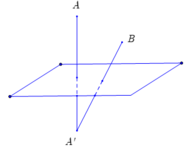
Ta có A, B cùng nằm về một phía của (P). Gọi A' đối xứng với A qua (P) suy ra A' (-2; 2; 1). Ta có MA + MB = MA' + MB ≥ BA'. Dấu bằng xảy ra khi M là giao điểm của BA' và (P). Xác định được 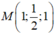 . Suy ra Chọn B
. Suy ra Chọn B

Chọn C
Gọi I là trung điểm của 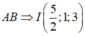
Ta có: ![]()
![]()
IA²+IB² không đổi nên MA²+MB² đạt giá trị nhỏ nhất khi MI đạt giá trị nhỏ nhất.
=> M là hình chiếu của I trên trục Oz.
=> M (0;0;3).