Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình mặt chắn của mặt phẳng (ABC) là: ![]()
Từ giả thiết 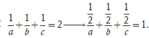 Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.
Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.

Đáp án A
Phương trình mặt phẳng A B C : x a + y b + z c = 1
Vì I ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 6 a b c 3 ⇔ a b c ≥ 162
Thể tích khối tứ diện OABC được tính là V = O A . O B . O C 6 = a b c 6 ≥ 162 6 = 27
Dấu “=” xảy ra khi 1 a = 2 b = 3 c = 1 3 ⇒ a = 3 b = 6 c = 9
Kiểm tra thấy phương án A không đúng




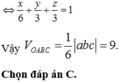




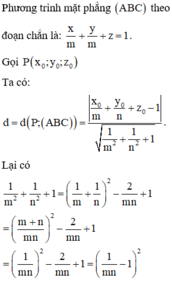
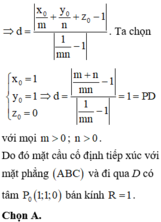
Đáp án A
Phương pháp:
+) Viết phương trình mặt phẳng (ABC) ở dạng đoạn chắn, thay tọa độ điểm M vào pt mặt phẳng (ABC).
+) (ABC) tiếp xúc với mặt cầu (S) tâm I bán kính R ó d(I;(ABC)) = R
Cách giải:
(ABC) tiếp xúc với mặt cầu (S) có tâm I(1;2;3) và bán kính R = 72 7