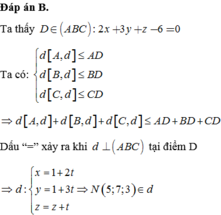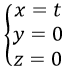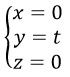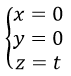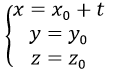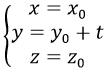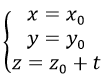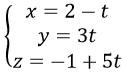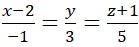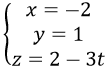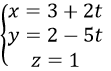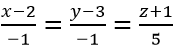Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Trục Ox là đường thẳng đi qua O(0, 0, 0) và nhận i→=(1,0,0) làm vectơ chỉ phương nên có phương trình tham số là:
* Tương tự, trục Oy có phương trình
Trục Oz có phương trình
b) Đường thẳng đi qua M0 (x0,y0,z0) song song với trục Ox sẽ có vectơ chỉ phương là i→(1,0,0) nên có phương trình tham số là:
tương tự ta có Phương trình của đường thẳng đi qua M0 (x0,y0,z0) và song song với Oy là:
phương trình đường thẳng đi qua M0 (x0,y0,z0) và song song với Oz là
c) Đường thẳng đi qua M(2, 0, -1) và có vectơ chỉ phương u→(-1,3,5) có phương trình tham số là
có phương trình chính tắc là
d) Đường thẳng đi qua N(-2, 1, 2) và có vectơ chỉ phương u→(0,0,-3) có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
e) Đường thẳng đi qua N(3, 2, 1) và vuông góc với mặt phẳng: 2x- 5y + 4= 0 nên nó nhận vectơ pháp tuyến của mặt phẳng này làn→(2,-5,0) là vectơ chỉ phương, nên ta có phương trình tham số là
Đường thẳng này không có Phương trình chính tắc.
f) Đường thẳng đi qau P(2, 3, -1) và Q(1, 2, 4) sẽ nhận PQ→(-1,-1,5) là vectơ chỉ phương, nên có phương trình tham số là
và có phương tình chính tắc là

Câu 1:
Do \(MA=MB\Rightarrow M\) là trung điểm AB
Gọi \(B\left(a;0;0\right)\) \(\Rightarrow\left\{{}\begin{matrix}x_A=2x_M-x_B=6-a\\y_A=2y_M-y_B=4\\z_A=2z_M-z_B=2\end{matrix}\right.\)
Mà \(A\in\left(Q\right)\)
\(\Rightarrow6-a+4+2-7=0\Rightarrow a=5\)
\(\Rightarrow\left\{{}\begin{matrix}B\left(5;0;0\right)\\A\left(1;4;2\right)\end{matrix}\right.\) \(\Rightarrow AB=6\)
Câu 2:
Gọi (Q) là mặt phẳng chứa A và song song (P)\(\Rightarrow d\in\left(Q\right)\)
Phương trình (Q):
\(2\left(x-1\right)+1\left(y-2\right)-4\left(z-3\right)=0\)
\(\Leftrightarrow2x+y-4z+8=0\)
Giao điểm B của (Q) và trục Ox: \(2x+8=0\Rightarrow x=-4\) \(\Rightarrow B\left(-4;0;0\right)\)
\(\Rightarrow d\) nhận \(\overrightarrow{u_d}=\overrightarrow{BA}=\left(5;2;3\right)\) là một vtcp
Phương trình d: \(\left\{{}\begin{matrix}x=-4+5t\\y=2t\\z=3t\end{matrix}\right.\)

Chọn D
Đường thẳng d đi qua A nên d (B; d) ≤ BA, do đó khoảng cách từ B đến d lớn nhất khi ![]() , với là vectơ chỉ phương của d.
, với là vectơ chỉ phương của d.


Quỹ tích d là hình trụ dài vô tận có trục là Oz và bán kính \(R=3\)
Khoảng cách từ A đến d là lớn nhất khi d đi qua giao điểm của đường thẳng d' và trụ, trong đó d' qua A, cắt đồng thời vuông góc Oz
\(\Rightarrow\) A đúng

Đáp án B.
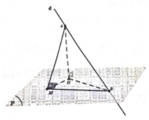
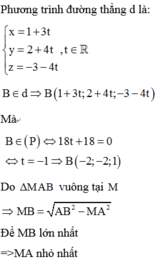
Gọi H là hình chiếu vuông góc của A lên mặt phẳng (P)
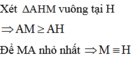
⇒ M B là giao tuyến của mặt phẳng (P) với mặt phẳng α ( α là mặt phẳng chứa d và vuông góc với mặt phẳng (P))
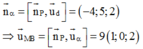
Vậy phương trình đường thẳng MB:
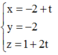
Thấy ngay điểm I(-1;-2;3) thỏa mãn.

Chọn D
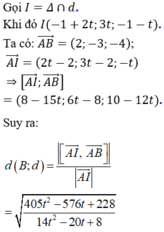
Xét hàm số:
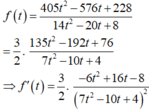
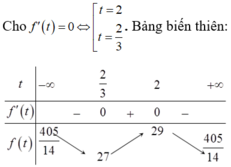
Do đó d (B; d) nhỏ nhất khi f(t) đạt giá trị nhỏ nhất bằng 27 tại t = 2/3. Suy ra ![]() . Chọn một vectơ chỉ phương của đường thẳng d là
. Chọn một vectơ chỉ phương của đường thẳng d là ![]()
Vậy phương trình đường thẳng ![]()