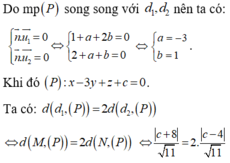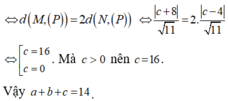Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(d_2:\left\{{}\begin{matrix}x=-1\\y=t\\z=-1+t\end{matrix}\right.\)
Gọi giao điểm của \(\Delta\) và \(d_2\) là A
\(\Rightarrow A\left(-1;a;-1+a\right)\Rightarrow\overrightarrow{MA}=\left(-1;a-1;a-2\right)\)
Do \(\Delta\perp d_1\Rightarrow\overrightarrow{MA}.\overrightarrow{u_{d1}}=0\)
\(\Leftrightarrow3.\left(-1\right)+4.\left(a-1\right)+1\left(a-2\right)=0\)
\(\Leftrightarrow5a-9=0\Rightarrow a=\frac{9}{5}\Rightarrow\overrightarrow{MA}=\left(-1;\frac{4}{5};\frac{-1}{5}\right)\)
Chọn \(\overrightarrow{u_{\Delta}}=\left(5;-4;1\right)\) là 1 vtcp của \(\Delta\)
\(\Rightarrow cos\alpha=\frac{\left|5.0-4.1+1.1\right|}{\sqrt{0+1+1}.\sqrt{25+16+1}}=\frac{\sqrt{21}}{14}\)
Kết quả xấu vậy ta

Câu 28:
\(\overrightarrow{CB}=\left(1;-1;1\right)\)
Do (P) vuông góc BC nên nhận (1;-1;1) là 1 vtpt
Phương trình (P):
\(1\left(x-1\right)-1\left(y-1\right)+1\left(z+5\right)=0\)
\(\Leftrightarrow x-y+z+5=0\)
Câu 29:
Mạt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên nhận các vecto có dạng \(\left(k;-2k;3k\right)\) cũng là các vtpt với \(k\ne0\)
Do đó đáp án B đúng (ko tồn tại k thỏa mãn)
Với đáp án A thì \(k=-2\) , đáp án C thì \(k=3\), đáp án D có \(k=1\)

Chọn D.
Ta có d1 đi qua A(2;2;3) và có ![]()
![]()
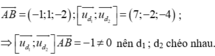
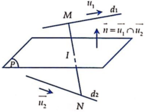
Do (P) cách đều d1;d2 nên (P) song song với d 1 , d 2
![]()
(P) có dạng 7x – 2y – 4z + d = 0
Vì (P) cách đều hai đường thẳng nên: d(A;(P)) = d(B;(P))
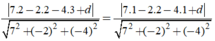
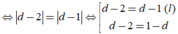
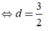
![]()
![]()
![]()

Bài 1:
ĐKXĐ:.............
Phương trình hoành độ giao điểm của \((d)\cap (C)\):
\(2(x-m)-\frac{2x-m}{mx+1}=0\Leftrightarrow m(2x^2-2mx-1)=0\)
Nếu \(m=0\Rightarrow (d)\equiv C\) (vô lý) nên $m\neq 0$ . Do đó \(2x^2-2mx-1=0\). $(1)$
Hai điểm $A,B$ có hoành độ chính là nghiệm của phương trình $(1)$
Áp dụng định lý Viet: \(\left\{\begin{matrix} x_1+x_2=m\\ x_1x_2=\frac{-1}{2}\end{matrix}\right.\)
\(d(O,AB)=\frac{|-2m|}{\sqrt{5}}\); \(AB=\sqrt{(x_1-x_)^2+(y_1-y_2)^2}=\sqrt{5(m^2+2)}\)
\(\Rightarrow S_{OAB}=\frac{d(O,AB).AB}{2}=|m|\sqrt{m^2+2}\)
Mặt khác, dễ dàng tính được \(M(m,0),N(0,-2m)\) nên \(S_{OMN}=\frac{OM.ON}{2}=\frac{|m||-2m|}{2}=m^2\)
Ta có \(S_{OAB}=3S_{OMN}\Leftrightarrow |m|\sqrt{m^2+2}=3m^2\)
\(\Rightarrow m=\pm \frac{1}{2}(m\neq 0)\)
Bài 2:
Ta có \(A(1,0,1)\in (d_1);B(3,5,4)\in (d_2); \overrightarrow{u_{d_1}}=(-1,1,1);\overrightarrow{u_{d_2}}=(4,-2,1)\)
Dễ thấy \([\overrightarrow{u_{d_1}},\overrightarrow{u_{d_2}}]\overrightarrow{AB}\neq 0\) nên suy ra $(d_1)$ và $(d_2)$ chéo nhau
Gọi \(\overrightarrow{n_P}\) là vector pháp tuyến của mặt phẳng $(P)$
Khi đó \(\overrightarrow{n_P}=[\overrightarrow{u_{d_1}},\overrightarrow{u_{d_2}}]=(3,5,-2)\)
Vì $(P)$ đi qua $(d_1)$ nên $(P)$ đi qua $A$. Do đó PTMP là:
\(3(x-1)+5y-2(z-1)=0\Leftrightarrow 3x+5y-2z-1=0\)