Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

làm đc chưa bạn...
gọiE là tđ AD
suy ra NA = NH = NMNM
gọi F là tđ AM thì c/m đc KN KM KA KD bằng nhau
vậy AMN cân vuông tại N

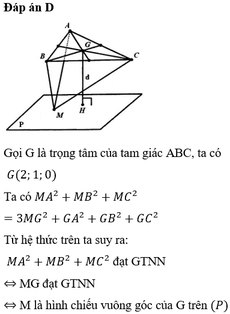
Đáp án D
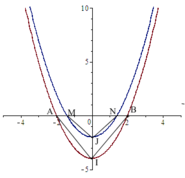
Phép tịnh tiến theo v → 0 ; b biến parabol P : y = x 2 − 4 thành parabol P ' : y = x 2 − 4 + b
Giao điểm của A,B với Ox của (P) có tọa độ lần lượt là: − 2 ; 0 , 2 ; 0
Giao điểm M,N với Ox của (P) có toạn độ lần lượt là: − 4 − b ; 0 , 4 − b ; 0
Đỉnh I,J của parabon (P), (P') có tọa độ lần lượt: 0 ; − 4 , 0 ; − 4 + b
Diện tích tam giác IAB bằng 8 lần diện tích tam giác JMN nên ta có:
I O . A B = 8 J O . M N ⇔ 4.4 = 8. 4 − b .2 4 − b ⇔ 4 − b 3 = 1 ⇔ b = 3 ⇒ J 0 ; − 1

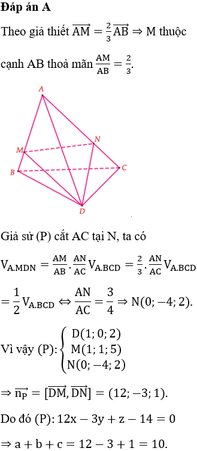
Đáp án A
Phương trình mặt phẳng A B C : x a + y b + z c = 1
Vì I ∈ A B C ⇔ 1 a + 2 b + 3 c ≥ 3 6 a b c 3 ⇔ a b c ≥ 162
Thể tích khối tứ diện OABC được tính là V = O A . O B . O C 6 = a b c 6 ≥ 162 6 = 27
Dấu “=” xảy ra khi 1 a = 2 b = 3 c = 1 3 ⇒ a = 3 b = 6 c = 9
Kiểm tra thấy phương án A không đúng

Đáp án C.
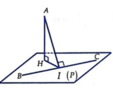
Ta có B C → = - 2 ; - 1 ; - 2 nên phương trình đường thẳng BC là x = 1 - 2 t y = - t ( t ∈ ℝ ) z = 2 - 2 t .
Gọi I là hình chiếu vuông góc của A trên BC, H là hình chiếu vuông góc của A trên mặt phẳng (P) . Khi đó A H = d A ; P ≤ A I và AH đạt giá trị lớn nhất khi H ≡ I . Suy ra mặt phẳng (P) qua I và vuông góc với AI.
Từ I ∈ B C ⇒ I 1 - 2 t ; - t ; 2 - 2 t và A I → = - 1 - 2 t ; - t - 5 ; - 1 - 2 t .
Lại có A I ⊥ B C ⇔ A I → . B C → = 0 ⇔ 2 ( 1 + 2 t ) + ( t + 5 ) + 2 ( 1 + 2 t ) = 0 ⇔ t = - 1 .
Mặt phẳng (P) đi qua I(3;1;4) và nhận VTPT là A I → = 1 ; - 4 ; 1 nên có phương trình tổng quát là: x - 4 y + z - 3 = 0 .
Vậy a = 1 , b = - 4 , c = 1 , d = - 3 → M = 1 + 1 - 4 - 3 = - 2 7 .
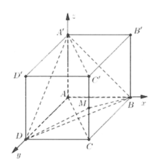
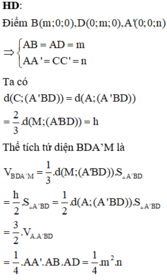



Đáp án là C.
+ Tìm được M m ; m ; n 2 .
+ Ta có:
B M → = 0 ; m ; n 2 ; B D → = − m ; m ; 0 ; B A ' → = − m ; 0 ; n
B M → ; B D → = − m n 2 ; − m n 2 ; m 2 ; B M → ; B D → B A ' → = 3 2 m 2 n
V B M D A ' = 1 6 B M → ; B D → B A ' → = 1 4 m 2 n
mà n = 4 − m ⇒ V B M D A ' = − 1 4 m 3 + m 2 = f m
+ f ' m = − 3 4 m 2 + 2 m = 0 ⇔ m = 0 l o a i m = 8 3 ⇒ f m = 64 27