Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Cách 1: Gọi A ( t ; 1 + 2 t ; 6 + 3 t ) và B 1 + t ' ; - 2 + t ' ; 3 - t ' lần lượt là giao điểm của ∆ với d và d'. Ta có: A B → = 1 + t ' - t ' ; - 3 + t ' - 2 t ; - 3 - t ' - 3 t .
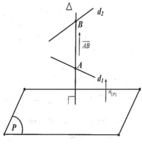
Vì ∆ song song với trục Oz mà trục Oz có vtcp k → = 0 ; 0 ; 1 .
Suy ra 1 + t ' - t = 0 - 3 + t ' - 2 t = 0 ⇔ t = - 4 t ' = - 5 .
Vậy A = - 4 ; - 7 ; - 6 . Do đó ∆ có phương trình tham số x = - 4 y = - 7 z = - 6 + t .
Cách 2: Trục Oz có vtcp u o z → = 0 ; 0 ; 1 .
Đường thẳng d đi qua M(0;1;6) và vtcp u d → = 1 ; 2 ; 3 .
Đường thẳng d' đi qua N(1;-2;3) và có vtcp u d ' → = 1 ; 1 ; - 1 .
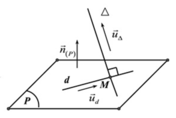
- Gọi (P) là mặt phẳng song song với trục Oz và chứa d : x 1 = y - 1 2 = z - 6 3
⇒ n ( P ) → = u O z → , u d → = - 2 ; 1 ; 0 .
Mặt phẳng (P) có phương trình - 2 x + ( y - 1 ) = 0 ⇔ - 2 x + y - 1 = 0 .
- Gọi Q là mặt phẳng song song với trục Oz và chứa d ' : x - 1 1 = y + 2 1 = z - 3 - 1 song song với trục Oz và chứa d ' = x - 1 1 = y + 2 1 = z - 3 - 1
⇒ n Q → = u O z → , u d ' → = - 1 ; 1 ; 0 .
Mặt phẳng Q có phương trình
- 1 ( x + 1 ) + 1 . ( y + 2 ) + 0 . ( z - 3 ) = 0 ⇔ - x + y + 3 = 0 .
- Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (P) và mặt phẳng Q .
Gọi A ∈ ∆ ⇒ A ∈ P , A ∈ P , A ∈ Q ⇒ A - 4 ; - 7 ; - 6 .
Đường thẳng ∆ có vtcp u ∆ → cùng phương với n P → , n Q → = 0 ; 0 ; - 1 .
⇒ ∆ : x = - 4 y = - 7 t ∈ ℝ z = - 6 + t .

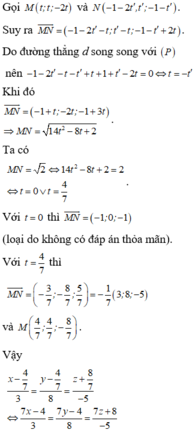








Đáp án C.