Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ta có \(\left|x-a\right|+\left|x-b\right|+\left|x-c\right|+\left|x-d\right|\ge\left|\left(x-a\right)+\left(x-b\right)+\left(c-x\right)+\left(d-x\right)\right|=\left|c+d-a-b\right|=c+d-a-b\)( do a<b<c<d => c-a>0 và d-b>0)
vậy Min A= c+d-a-b

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

Đáp án C
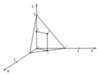
Phương pháp: Sử dụng phương pháp xác định tâm mặt cầu ngoại tiếp khối chóp.
Cách giải: Đặt A(x;0;0), B(0;y;0), (x,y > 0)
Vì OA + OB = OC = 1 => x + y = 1
Gọi J, F lần lượt là trung điểm AB, OC. Kẻ đường thẳng qua F song song OJ, đường thẳng qua J song song OC, 2 đường thẳng này cắt nhau tại G.
∆OAB vuông tại O => J là tâm đường tròn ngoại tiếp tam giác.
GJ // OC => GJ ⊥ (OAB) => GO = GA = GB
GF // JO, JO ⊥ OC => GF ⊥ OC, mà F là trung điểm của OC
=>GF là đường trung trực của OC => GC = GO
=> GO = GA = GB = GC => G là tâm mặt cầu ngoại tiếp tứ diện OABC
Bán kính mặt cầu ngoại tiếp tứ diện OABC :
![]()
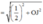
Ta có:
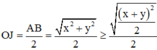
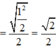
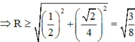
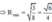

a,Nx: (x+1)2008>=0 với mọi x
=>20- (x+1)2008< hoặc = 20
=> GTLN của A là 20 tại (x+1)2008=0
=> x+1=0
=> x=-1
Vậy GTLN của A là 20
b,Nx: /3-x/> hoặc= 0 với mọi x
=>1010-/3-x/ < hoặc = 0
=>GTLN của B là 1010 tại /3-x/=0
=>3-x=0
=>x=3
c, Nx : (x-1)2 > hoặc = 0
=> (x-1)2 +90 > hoặc = 90
=> GTNN của C là 90 tại (x-1)2=0
=> x-1=0
=> x=1
Vậy GTNN của C là 90
d, Nx: /x+4/> hoặc =0
=> /x+4/ +2015 > hoặc = 2015 với mọi x
=>GTNN của D là 2015 tại /x+4/=0
=> x+4=0
=> x= -4
Vậy GTNN của D là 2015

\(3+\frac{1}{4+\frac{1}{b+\frac{1}{6}}}=\frac{421}{130}\) \(\Rightarrow\frac{1}{4+\frac{1}{b+\frac{1}{6}}}=\frac{31}{130}\Rightarrow4+\frac{1}{b+\frac{1}{6}}=\frac{130}{31}\Rightarrow\frac{1}{b+\frac{1}{6}}=\frac{6}{31}\Rightarrow b+\frac{1}{6}=\frac{31}{6}\Rightarrow b=\frac{30}{6}=5\)
Vậy b = 5






Giả sử
Tứ diện OABC có OA, OB, OC đôi một vuông góc.
Gọi M, N lần lượt là trung điểm của AB và OC.
Ta có
Qua M dựng đường thẳng song song với OC, qua N dựng đường thẳng song song với OM. Hai đường thẳng này cắt nhau tại I.
∆ O A B vuông tại O ⇒ M là tâm đường tròn ngoại tiếp ∆ O A B ⇒ I A = I B = I O .
I là tâm mặt cầu ngoại tiếp O.ABC
Ta có
Chọn A.