Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án B
Đường thẳng ∆ có vecto chỉ phương u → (2; -3; 2)
Đường thẳng d đi qua M(4;3;1) và song song với đường thẳng ∆ nên có vecto chỉ phương là u → (2; -3; 2). Phương trình chính tắc của đường thẳng d là:
a: (d) vuông góc (d1)
=>(d): x+2y+c=0
Thay x=-1 và y=4 vào (d),ta được:
c-1+8=0
=>c=-7
=>(d): x+2y-7=0
=>VTPT là (1;2) và (d) đi qua A(-1;4)
=>VTCP là (-2;1) và (d) đi qua A(-1;4)
PTTS là:
x=-1-2t và y=4+t
b: (d1): x=1-2t và y=4+t
=>VTCP là (-2;1)
=>PTTS của (d) là:
x=-4-2t và y=3+t
VTCP là (-2;1)
=>VTPT là (1;2)
Phương trình (d) là:
1(x+4)+2(y-3)=0
=>x+4+2y-6=0
=>x+2y-2=0
c: (d1): x=2-3t và y=2+2t
=>VTCP là (-3;2)
=>VTPT của (d) là (-3;2)
PTTQ của (d) là:
-3(x+1)+2(y-3)=0
=>-3x-3+2y-6=0
=>-3x+2y-9=0
=>VTCP là (2;3)
PTTS là:
x=-1+2t và y=3+3t
Đáp án A
*Gọi (Q) là mặt phẳng chứa d và vuông góc với mặt phẳng (Oxy). Để khoảng cách giữa hai đường thẳng d và ∆ nhỏ nhất thì ∆ chính là giao tuyến của hai mặt phẳng (Oxy) và mp (Q).
* Mặt phẳng (Oxy) có phương trình là z = 0 có VTPT n Oxy → = (0; 0; 1).
Đường thẳng d đi qua A(1;2; -3) và có VTCP u d → = (1; -2; 0)
Suy ra, VTPT của (Q) là n Q → = [ u d → ; n Oxy → ] = (2; 1; 0)
Phương trình mặt phẳng (Q) là: 2(x - 1) + 1(y - 2) + 0(z + 3) = 0
Hay 2x + y -4 =0
* Đường thẳng ∆ cần tìm là giao tuyến của hai mặt phẳng (Oxy) và (Q). Tập hợp các điểm thuộc ∆ là nghiệm hệ phương trình: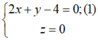 
* Đặt x = 1 + t thay vào (1) ta được: y = 4 - 2x = 4 - 2(1 + t) = 2 - 2t
Suy ra, phương trình tham số của đường thẳng ∆ là: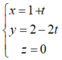 
a) Xét phương trình tham số của d: \(\left\{ \begin{array}{l}x = - 1 - 3t\left( 1 \right)\\y = 2 + 2t\left( 2 \right)\end{array} \right.\).
Lấy \(\left( 1 \right) + \frac{3}{2}.\left( 2 \right) \Rightarrow x + \frac{3}{2}y = 2 \Rightarrow 2x + 3y - 4 = 0\)
Vậy phương trình tổng quát của đường thẳng d là: \(2x + 3y - 4 = 0\)
b) Xét hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y - 4 = 0\\x = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = \frac{4}{3}\\x = 0\end{array} \right.\) . Vậy giao điểm của d với trục Oy là: \(A\left( {0;\frac{4}{3}} \right)\)
Xét hệ phương trình: \(\left\{ \begin{array}{l}2x + 3y - 4 = 0\\y = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = 2\end{array} \right.\) . Vậy giao điểm của d với trục Ox là: \(B\left( {2;0} \right)\)
c) Thay tọa độ điểm \(M\left( { - 7;{\rm{ }}5} \right)\)vào phương trình đường thẳng d ta có: \(2.\left( { - 7} \right) + 3.5 - 4 \ne 0\)
Vậy \(M\left( { - 7;{\rm{ }}5} \right)\)không thuộc đường thẳng d.
2.
Đường thẳng d có 1 vtcp là \(\left(-2;3\right)\) hoặc \(\left(2;-3\right)\) cũng được
7.
Phương trình tham số của d: \(\left\{{}\begin{matrix}x=1-4t\\y=-4+9t\end{matrix}\right.\)
Chắc là đề bài thiếu dữ kiện, do có vô số đường thẳng song song với d, tất cả những đường thẳng có dạng \(3x+2y+c=0\) với \(c\ne-11\) đều thỏa mãn yêu cầu
và song song với mặt phẳng (P): 2x - 3y + z - 2 = 0.
Đáp án B
Từ giả thiết suy ra
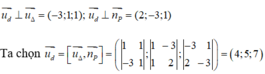
Mặt khác đường thẳng d đi qua điểm M(2;-1;1) nên phương trình tham số của đường thẳng d là: x = 2+ 4t, y = -1, + 5t, z = 1 + 7t.
Vậy đáp án đúng là B.
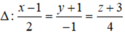
Đáp án C