Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Với điểm M(1;-2;3). Gọi M 1 , M 2 , M 3 lần lượt là hình chiếu vuông góc của điểm M trên các trục Ox, Oy, Oz thì tọa độ M 1 (1; 0; 0); M 2 (0 ;-2; 0) và M 3 ( 0; 0; 3).
Phương trình mặt phẳng M1M2M3 là:
x 1 + y - 2 + z 3 = 1

Giải:
a) Gọi (α) là mặt phẳng qua P và chứa trục Ox, thì (α) qua điểm O(0 ; 0 ; 0) và chứa giá của các vectơ (4 ; -1 ; 2) và
( 1 ; 0 ;0). Khi đó
=(0 ; 2 ; 1) là vectơ pháp tuyến của (α).
Phương trình mặt phẳng (α) có dạng: 2y + z = 0.
b) Tương tự phần a) mặt phẳng (β) qua điểm Q(1 ; 4 ; -3) và chứa trục Oy thì (β) qua điểm O( 0 ; 0 ; 0) có (1 ; 4 ; -3) và
(0 ; 1 ; 0) là cặp vectơ chỉ phương.
Phương trình mặt phẳng (β) có dạng : 3x + z = 0.
c) Mặt phẳng (ɣ) qua điểm R(3 ; -4 ; 7) và chứa trục Oz chứa giá của các vectơ
(3 ; -4 ; 7) và
(0 ; 0 ; 1) nhận 2 vectơ này làm vectơ chỉ phương.
Phương trình mặt phẳng (ɣ) có dạng :4x + 3y = 0.

Lần sau em đăng trong h.vn
1. \(log_{ab}c=\frac{1}{log_cab}=\frac{1}{log_ca+log_cb}=\frac{1}{\frac{1}{log_ac}+\frac{1}{log_bc}}=\frac{1}{\frac{log_ac+log_bc}{log_ac.log_bc}}=\frac{log_ac.log_bc}{log_ac+log_bc}\)
Đáp án B:
2. \(f'\left(x\right)=-4x^3+8x\)
\(f'\left(x\right)=0\Leftrightarrow-4x^3+8x=0\Leftrightarrow x=0,x=\sqrt{2},x=-\sqrt{2}\)
Có BBT:
x -căn2 0 căn2 f' f 0 0 0 - + - +
Nhìn vào bảng biên thiên ta có hàm số ... là đáp án C

Chọn D
Tứ diện OABC có ba cạnh đôi một vuông góc không phải là hình chóp đều.

Đáp án D.
Gọi A, B, C lần lượt là hình chiếu của M trên các trục Ox, Oy, Oz.
Suy ra A(1;0;0), B(0;2;0), C(0;0;3)
Phương trình:
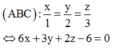

\(\overrightarrow{AB}=\left(-1;-2;1\right)\); \(\overrightarrow{n_{\alpha}}=\left(2;-1;2\right)\)\(\Rightarrow\overrightarrow{n_p}=\left[\overrightarrow{AB};\overrightarrow{n_{\alpha}}\right]=\left(-3;4;5\right)\)
Phương trình mặt phẳng (P) : \(-3x+4y+5z=0\)
\(R=d\left(A;\left(\alpha\right)\right)=\frac{\left|6-1+2+1\right|}{\sqrt{9}}=\frac{8}{3}\)
Phương trình mặt cầu (S) : \(\left(x-3\right)^2+\left(y-1\right)^2+\left(z-1\right)^2=\frac{64}{9}\)

câu 5 ấy chắc thầy tui buồn ngủ nên quánh lộn chữ sai thành đúng r
12.
\(R=d\left(I;Oxz\right)=\left|y_I\right|=3\)
Phương trình:
\(x^2+\left(y+3\right)^2+z^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+6y=0\)
13.
\(R=d\left(M;\alpha\right)=\frac{\left|1-1+2.2-3\right|}{\sqrt{1^2+1^2+2^2}}=\frac{1}{\sqrt{6}}\)
Pt mặt cầu:
\(\left(x-1\right)^2+\left(y-1\right)^2+\left(z+2\right)^2=\frac{1}{6}\)
14.
\(R=d\left(I;\left(P\right)\right)=\frac{\left|-1-4-2-2\right|}{\sqrt{1^2+2^2+2^2}}=3\)
Phương trình:
\(\left(x+1\right)^2+\left(y-2\right)^2+\left(z-1\right)^2=9\)
\(\Leftrightarrow x^2+y^2+z^2+2x-4y-2z-3=0\)

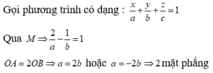
Đáp án C
Vì A 1 , A 2 , A 3 lần lượt là hình chiếu vuông góc của điểm A(4;3;2) lên các trục Ox, Oy, Oz nên ta có A 1 (4; 0; 0), A 2 (0; 3; 0), A 3 (0; 0; 2).
Từ đó suy ra các khẳng định A và B là đúng.
Thể tích của khối tứ diện
Vậy khẳng định C là đúng.