Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi (P) là mặt phẳng qua I và vuông góc với d \(\Rightarrow\left(P\right)\) có một vtpt \(\overrightarrow{n_{\left(P\right)}}=\overrightarrow{u_d}=\left(2;-2;1\right)\)
\(\Rightarrow\) phương trình (P): \(2\left(x-4\right)-2\left(y-1\right)+1\left(z-6\right)=0\)
\(\Leftrightarrow2x-2y+z-12=0\)
Gọi M là giao điểm của d và (P) \(\Rightarrow IM\perp d\), pt tham số của d: \(\left\{{}\begin{matrix}x=-2+2t\\y=7-2t\\z=t\end{matrix}\right.\)
Thay vào pt (P) ta được \(2\left(-2+2t\right)-2\left(7-2t\right)+t-12=0\) \(t=\dfrac{10}{3}\)
\(\Rightarrow\) tọa độ \(M\left(\dfrac{14}{3};\dfrac{1}{3};\dfrac{10}{3}\right)\)
\(\Rightarrow IM=\sqrt{\left(4-\dfrac{14}{3}\right)^2+\left(1-\dfrac{1}{3}\right)^2+\left(6-\dfrac{10}{3}\right)^2}=2\sqrt{2}\)
Do d cắt mặt cầu tại A, B nên M là trung điểm của AB \(\Rightarrow MA=\dfrac{AB}{2}=3\)
Trong tam giác \(IMA\) vuông tại M, áp dụng Pitago:
\(R=IA=\sqrt{IM^2+MA^2}=\sqrt{9+8}=\sqrt{17}\)
\(\Rightarrow\) pt mặt cầu (S): \(\left(x-4\right)^2+\left(y-1\right)^2+\left(z-6\right)^2=17\)

Mặt phẳng (P) qua A và vuông góc d có phương trình:
\(2\left(x-1\right)+2\left(y+1\right)+1\left(z-1\right)=0\)
\(\Leftrightarrow2x+2y+z-1=0\)
Đường thẳng d' song song d và đi qua B (nên d' vuông góc (P)) có dạng:
\(\left\{{}\begin{matrix}x=4+2t\\y=2+2t\\z=-2+t\end{matrix}\right.\)
\(\Rightarrow\) Giao điểm C của d' và (P) thỏa mãn:
\(2\left(4+2t\right)+2\left(2+2t\right)-2+t-1=0\Rightarrow t=-1\Rightarrow C\left(2;0;-3\right)\)
\(\Rightarrow\overrightarrow{AC}=\left(1;1;-4\right)\Rightarrow\) là 1 vtcp của \(\Delta\Rightarrow\) D là đáp án đúng

Chọn C
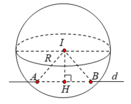
Gọi R là bán kính của mặt cầu, H là trung điểm của AB.
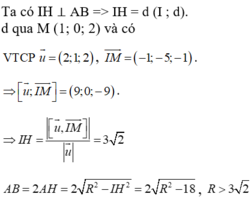
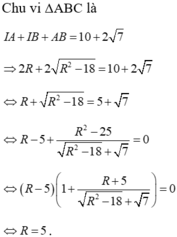
Mặt cầu (S) có tâm I (2; 5; 3), bán kính R = 5.
Phương trình mặt cầu (S) là: ![]()
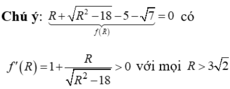
nên phương trình có nghiệm duy nhất R=5.

Chọn A
Đường thẳng d đi qua M(-5;7;0) và có vectơ chỉ phương ![]()
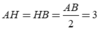
Gọi H là hình chiếu của I lên (d). Ta có:
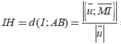
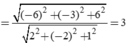
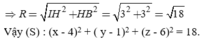

Lời giải:
Dễ thấy đường thẳng $d_1$ đi qua điểm \(M(1,-1,0)\Rightarrow \overrightarrow{MA}=(4,-2,5)\)
Khi đó, nếu $(P)$ là mp chứa \(d_1,MA\) thì \(\overrightarrow{n_P}=[\overrightarrow{d_1},\overrightarrow{MA}]=(1,-3,-2)\)
\(\Rightarrow \text{PTMP}: x-3y-2z-4=0\)
Ta thấy \(C\in (d_2),C\in (P)\Rightarrow \) dễ dàng tìm được tọa độ điểm \(C(-1,-1,-1)\)
Lại có \(B=AC\cap d_1\). Và PTĐT \(AC\): \(\frac{x+1}{3}=\frac{y+1}{-1}=\frac{z+1}{3}\)
\(\Rightarrow B(2,-2,2)\)
Do đó \(BC=\sqrt{19}\)





I A B H
a)
Viết pt đường thẳng d dạng:
\(d=\left\{\begin{matrix}x=1+2t\\y=-1+t\\z=1+2t\end{matrix}\right.\)
Gọi \(H\left(1+2h;-1+h;1+2h\right)\) là hình chiếu vuông góc của I trên d
Ta có:
\(\overrightarrow{IH}\perp\overrightarrow{u_d}\Leftrightarrow\left(2h;-1+h;-2+2h\right)\left(2;1;2\right)=0\\ \Leftrightarrow9h-5=0\Leftrightarrow h=\frac{5}{9}\)
\(\overrightarrow{IH}=\left(\frac{10}{9};-\frac{4}{9};-\frac{8}{9}\right)\Rightarrow IH=\frac{2\sqrt{5}}{3}\)
b)
\(\Delta IAB\) vuông tại I và có đường cao IH, lại có IA=IB=R (R là bán kính mặt cầu (S))
Suy ra tam giác IAB vuông cân tại I \(\Rightarrow IA=IH\sqrt{2}=\frac{2\sqrt{10}}{3}\)
\(\Rightarrow R=\frac{2\sqrt{10}}{3}\)
Vậy \(\left(S\right):\left(x-1\right)^2+y^2+\left(z-3\right)^2=\frac{40}{9}\)
(Mình tính toán có thể sai, bạn tham khảo tạm cách làm nhé)