Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D H K S
Hạ \(SH\perp BC\Rightarrow\left(SBC\right)\perp\left(ABC\right)\)
\(\Rightarrow SH\perp BC;SH=SB.\sin\widehat{SBC}=a\sqrt{3}\)
Diện tích : \(S_{ABC}=\frac{12}{\boxtimes}BA.BC=6a^2\)
Thể tích : \(V_{s.ABC}=\frac{1}{3}S_{ABC}.SH=2a^3\sqrt{3}\)
Hạ \(HD\perp AC\left(D\in AC\right),HK\perp SD\left(K\in SD\right)\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H,\left(SAC\right)\right)\)
\(BH=SB.\cos\widehat{SBC}=3a\Rightarrow BC=4HC\)
\(\Rightarrow d\left(B,\left(SAC\right)\right)=4d\left(H,SAC\right)\)
Ta có : \(AC=\sqrt{BA^2+BC^2}=5a;HC=BC-BH=a\)
\(\Rightarrow HD=BA.\frac{HC}{AC}=\frac{3a}{5}\)
\(HK=\frac{SH.HS}{\sqrt{SH^2+HD^2}}=\frac{3a\sqrt{7}}{14}\)
Vậy \(d\left(B,\left(SAC\right)\right)=4HK=\frac{6a\sqrt{7}}{7}\)

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

Khoảng cách từ A đến mặt phẳng (P) là :
\(h=d_{\left(A,\left(P\right)\right)}=\frac{\left|1.2+\left(-2\right).\left(-2\right)+2.1+5\right|}{\sqrt{1^2+\left(-2\right)^2+2^2}}=4\)
Gọi r là bán kính của đường tròn thiết diện thì ta có \(2\pi r=6\pi\Rightarrow r=3\)
Gọi R là bán kính mặt cầu cần tìm, ta có : \(R^2=h^2+r^2=4^2+3^2=25\)
Vậy phương trình mặt cầu cần tìm là : \(\left(x-1\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=25\)

Chọn D
Xét tứ diện OABC có OA, OB, OC đôi một vuông góc nên nếu M là trực tâm tam giác ABC thì OM ⊥ (ABC)
Khi đó phương trình mặt phẳng (ABC) là: 2 (x-2)+ (y-1)+5 (z-5) = 0 ó 2x + y + 5z – 30 = 0.
Vậy khoảng cách từ điểm I (1;2;3) đến mặt phẳng (P) là 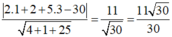

B C A D H K J S
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)


Đáp án D
Kiến thức: Chóp tam giác có 3 cạnh bên đôi một vuông góc với nhau thì hình chiếu của đỉnh trên mặt đáy trùng với trực tâm của đáy.
Chóp O.ABC có các cạnh OA, OB, OC đôi một vuông góc với nhau, M(2;1;5) là trực tâm của tam giác ABC
vậy (P) nhận O M → =(2;1;5) làm một vectơ pháp tuyến.
=> Phương trình mặt phẳng (P) là: 2(x-2)+y-1+5(z-5)=0
<=> 2x+y+5z-30=0