Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng cách từ A đến mặt phẳng (P) là :
\(h=d_{\left(A,\left(P\right)\right)}=\frac{\left|1.2+\left(-2\right).\left(-2\right)+2.1+5\right|}{\sqrt{1^2+\left(-2\right)^2+2^2}}=4\)
Gọi r là bán kính của đường tròn thiết diện thì ta có \(2\pi r=6\pi\Rightarrow r=3\)
Gọi R là bán kính mặt cầu cần tìm, ta có : \(R^2=h^2+r^2=4^2+3^2=25\)
Vậy phương trình mặt cầu cần tìm là : \(\left(x-1\right)^2+\left(y+2\right)^2+\left(z-1\right)^2=25\)

Lời giải:
Thiết diện là một tam giác đều cạnh \(a\sqrt{3}\) nên \(2R=\sqrt{3}a\Rightarrow R=\frac{\sqrt{3}a}{2}\)
Do đó diện tích xq của hình nón là:
\(S_{xq}=\pi Rl=\frac{3a^2}{2}\pi\)
Đáp án C

B C A D H K J S
Kẻ \(SH\perp AC\left(H\in AC\right)\)
Do \(\left(SAC\right)\perp\left(ABCD\right)\Rightarrow SH\perp\left(ABCD\right)\)
\(SA=\sqrt{AC^2-SC^2}=a;SH=\frac{SA.SC}{AC}=\frac{a\sqrt{3}}{2}\)
\(S_{ABCD}=\frac{AC.BD}{2}=2a^2\)
\(V_{S.ABCD}=\frac{1}{3}SH.S_{ABCD}=\frac{1}{3}.\frac{a\sqrt{3}}{2}.2a^2=\frac{a^3\sqrt{3}}{3}\)
Ta có \(AH=\sqrt{SA^2-SH^2}=\frac{a}{2}\Rightarrow CA=4HA\Rightarrow d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Do BC//\(\left(SAD\right)\Rightarrow d\left(B,\left(SAD\right)\right)=d\left(C,\left(SAD\right)\right)=4d\left(H,\left(SAD\right)\right)\)
Kẻ \(HK\perp AD\left(K\in AD\right),HJ\perp SK\left(J\in SK\right)\)
Chứng minh được \(\left(SHK\right)\perp\left(SAD\right)\) mà \(HJ\perp SK\Rightarrow HJ\perp\left(SAD\right)\Rightarrow d\left(H,\left(SAD\right)\right)=HJ\)
Tam giác AHK vuông cân tại K\(\Rightarrow HK=AH\sin45^0=\frac{a\sqrt{2}}{4}\)
\(\Rightarrow HJ=\frac{SH.HK}{\sqrt{SH^2+HK^2}}=\frac{a\sqrt{3}}{2\sqrt{7}}\)
Vậy \(d\left(B,\left(SAD\right)\right)=\frac{2a\sqrt{3}}{\sqrt{7}}=\frac{2a\sqrt{21}}{7}\)

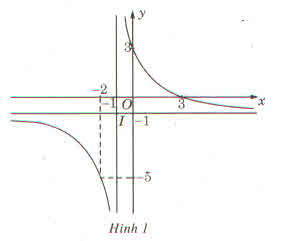
a) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)

Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$

19.
Phương trình mặt phẳng theo đoạn chắn:
\(\frac{x}{3}+\frac{y}{-4}+\frac{z}{-2}=1\)
\(\Leftrightarrow4x-3y-6z-12=0\)
20.
Phương trình mặt phẳng (ABC) theo đoạn chắn:
\(\frac{x}{1}+\frac{y}{2}+\frac{z}{3}=1\)
\(\Leftrightarrow6x+3y+2z-6=0\)
Chẳng đáp án nào đúng cả, chắc bạn ghi nhầm đáp án C số 1 thành số 0 :)
15.
\(2\left(x-2\right)-5\left(y+3\right)+1\left(z+2\right)=0\)
16.
\(\overrightarrow{n_1}=\left(1;1;-1\right)\) ; \(\overrightarrow{n_2}=\left(1;-1;1\right)\)
\(\left[\overrightarrow{n_1};\overrightarrow{n_2}\right]=\left(0;-2;-2\right)=-2\left(0;1;1\right)\)
Phương trình (P):
\(1\left(y-1\right)+1\left(z-1\right)=0\Leftrightarrow y+z-2=0\)
17.
\(\overrightarrow{n_P}=\left(1;-1;1\right)\) ; \(\overrightarrow{n_Q}=\left(3;2;-12\right)\)
\(\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(10;15;5\right)=5\left(2;3;1\right)\)
Phương trình mặt phẳng (R):
\(2x+3y+z=0\)
18.
\(\overrightarrow{MN}=\left(0;-2;3\right);\overrightarrow{MP}=\left(-2;1;3\right)\)
\(\left[\overrightarrow{MN};\overrightarrow{MP}\right]=\left(-9;-6;-4\right)=-1\left(9;6;4\right)\)
Phương trình:
\(9\left(x-2\right)+6\left(y-2\right)+4z=0\)
\(\Leftrightarrow9x+6y+4z-30=0\)
Đáp án A
Sử dụng phương trình mặt phẳng theo đoạn chắn, ta có phương trình mặt phẳng