Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

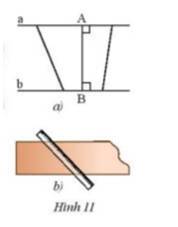
a) Chiều rộng của thanh nẹp gỗ là khoảng cách ngắn nhất từ một điểm trên cạnh này đến một điểm trên cạnh kia (đoạn vuông góc là đoạn ngắn nhất )
b) Ta đặt thước vuông góc với 2 cạnh của nẹp vì chiều rộng của thanh nẹp là khoảng cách giữa 2 cạnh của nẹp

Mục đích của việc này là giúp người thợ mộc quan sát xem gố bào đã nhẵn, phẳng hay chưa.
Để giải thích, người ta đã sử dụng định luật truyền thẳng của ánh sáng (vì không khí la môi trường trong suất nên ánh sáng truyền đi theo đường thẳng => nếu mặt gỗ đã nhẵn thì người thợ gỗ chỉ nhìn thấy 1 đầu của khúc gỗ ).
Mục đích của việc này là giúp người thợ mộc quan sát xem gố bào đã nhẵn, phẳng hay chưa.
Để giải thích, người ta đã sử dụng định luật truyền thẳng của ánh sáng (vì không khí la môi trường trong suất nên ánh sáng truyền đi theo đường thẳng => nếu mặt gỗ đã nhẵn thì người thợ gỗ chỉ nhìn tháy 1 đầu của khúc gỗ ).

Số cách rút ngẫu nhiên 2 thẻ khác nhau trong hộp là:
\(A^2_4=12\left(cách\right)\)
TH1: hai thẻ rút ra đều là số chẵn
Thẻ đầu tiên có 2 cách rút
Thẻ thứ hai có 1 cách rút
=>Có 2*1=2 cách rút
TH2: Trong hai thẻ rút ra có 1 thẻ chẵn, 1 thẻ lẻ
Số cách rút ra 1 thẻ chẵn là 2 cách
Số cách rút ra 2 thẻ chẵn là 2 cách
=>Có 2*2=4 cách rút
Tổng số cách để tích hai thẻ rút ra là số chẵn là:
2+4=6(cách)
Xác suất để rút ra hai thẻ có tích là số chẵn là:
\(\dfrac{6}{12}=\dfrac{1}{2}\)

Số chấm trên 1 con xúc xắc chỉ có thể là 1;2;3;4;5 hoặc 6
- Biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 13” là biến cố chắc chắn nên biến cố có xác suất là 1.
- Biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 1” là biến cố không thể nên biến cố có xác suất là 0.

Hai thanh chì có thể tích là 13 cm3 và 21 cm3 . Hai thanh có khối lượng hơn kém nhau 99,2g . Khối lượng của thanh nhỏ là 161,2 gam
Câu hỏi của nguyen bang nhan - Toán lớp 7 - Học toán với OnlineMath

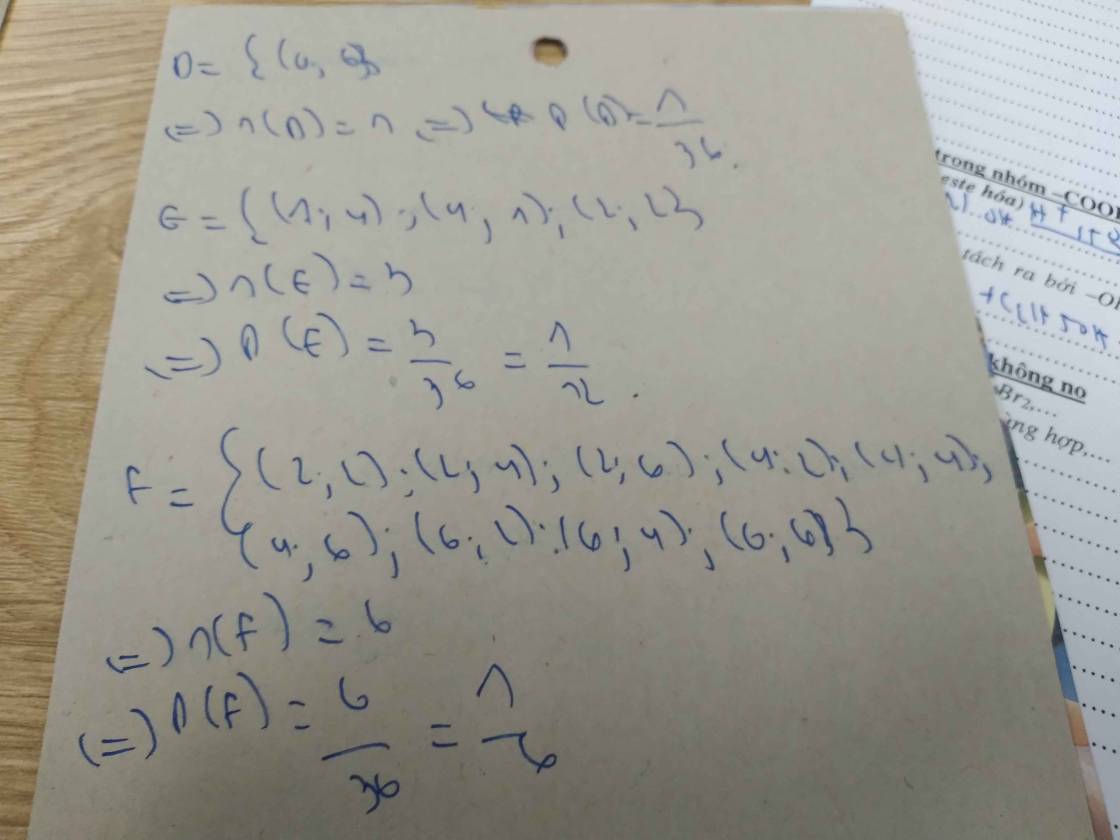
A là biến cố chắc chắn
=>P(A)=1
B là biến cố ko thể
=>P(B)=0
C={(3;1);(4;1);(4;2);(5;1);(5;2);(5;3);(6;1);(6;2);(6;3);(6;4)}
=>n(C)=10
=>P(C)=10/30=1/3
Biến cố D là biến cố chắc chăn
=>P(D)=1
E là biến cố ko thể
=>P(E)=0
n(F)=3*2=6
=>P(F)=6/30=1/5