Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
.
.
.
.
- Số cách lấy ngẫu nhiên 2 quả cầu: \(n\left( \Omega \right) = C_9^2 = 36\)
- Số cách lấy 2 quả khác màu là:
+ 1 quả màu xanh và 1 quả màu vàng: \(C_4^1 \times C_3^1 = 12\)
+ 1 quả màu xanh và 1 quả màu đỏ: \(C_4^1 \times C_2^1 = 8\)
+ 1 quả màu đỏ và 1 quả màu vàng: \(C_2^1 \times C_3^1 = 6\)
=> Tổng số cách lấy ra 2 quả khác màu là: 26 cách
- Số cách lấy 2 quả khác màu trùng số:
+ 2 quả cùng là số 1: \(C_3^2 = 3\)
+ 2 quả cùng là số 2: \(C_3^2 = 3\)
+ 2 quả cùng là số 3: \(C_2^2 = 1\)
=> Tổng số cách lấy ra 2 quả khác màu trùng số là: 7 cách
=> Số cách lấy ra 2 quả khác màu khác số là: 26 – 7 = 19 (cách)
=> Xác suất để lấy ra 2 quả khác màu khác số là: \(P = \frac{{19}}{{36}}\)
Đáp án A
Gọi 
là không gian mẫu.
Ta có 
Gọi D là biến cố: lấy được 2 quả cầu không trắng.
Ta có
a, Gọi T là biến cố "Trong 4 quả lấy ra có 3 quả cầu trắng".
\(\left|\Omega\right|=C^4_{15}\)
\(\left|\Omega_T\right|=C^3_7.C^1_8\)
\(\Rightarrow P\left(T\right)=\dfrac{\left|\Omega_T\right|}{\left|\Omega\right|}=\dfrac{C^3_7.C^1_8}{C^4_{15}}=\dfrac{8}{39}\)
Số cách chọn hai quả cầu cùng màu là:
\(5\cdot4+3\cdot2=26\left(cách\right)\)
Số quả cầu tất cả là 5+3=8(quả)
Xác suất để chọn hai quả cầu cùng màu là:
\(\dfrac{26}{8\cdot7}=\dfrac{13}{28}\)
Chọn A
Số cách lấy ra 6 quả cầu từ 10 quả cầu là
Gọi A là biến cố ‘‘Trong 6 quả cầu lấy ra có không quá 1 quả cầu trắng”.
Số cách lấy 4 quả cầu từ 6quả cầu đỏ và vàng là
.
Số cách lấy 2 quả cầu trắng là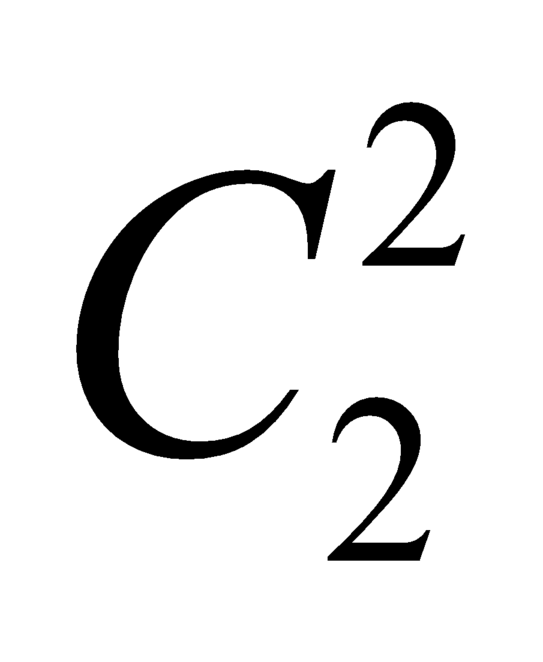
.
Theo quy tắc nhân ta có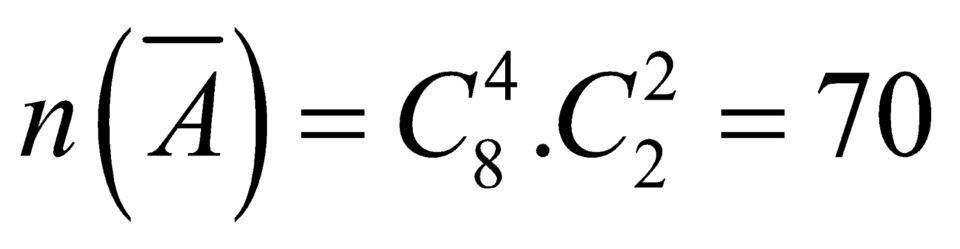
.
Vậy xác suất