K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

CM
8 tháng 10 2018
Vì ABCD là hình bình hành nên ∠ ABC = ∠ ADC.
Mặt khác, BE và DF lần lượt là phân giác của các góc B và D, do đó suy ra ∠ ADF = ∠ CBE
Mặt khác, ta có: AD = CB = b;
∠ DAF = ∠ BCE (so le trong)
Suy ra: △ ADF = △ CBE (g.c.g)
⇒ AF = CE
Đặt AF = CE = x
Theo tính chất của đường phân giác BE trong tam giác ABC, ta có: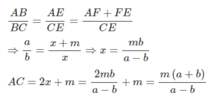
Thay số, tính trên máy tính điện tử cầm tay ta được: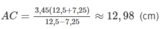

10 tháng 4 2023
a: Xet ΔEAD và ΔEBF có
góc EAD=góc EBF
góc AED=góc BEF
=>ΔEAD đồng dạng với ΔEBF
=>AD/BF=EA/EB
=>18/BF=9/6=3/2
=>BF=12cm