
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hướng dẫn giải:
∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có
S∆OBC = SΔOBC=R2√34 (1)
Diện tích hình quạt tròn AOB là:
π.R2.6003600=πR26 (2)
Từ (1) và (2) suy ra diện tích hình viên phân là:
πR26−R2√34=R2(π6−√34)
Thay R = 5,1 ta có Sviên phân ≈ 2,4 (cm2)

Giải:
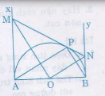
a) Ta có OM, ON lần lượt là tia phân giác cả AOP và BOP
Mà AOP kể bù BOP nên suy ra OM vuông góc với ON.
Vậy ∆MON vuông tại O.
Lại có ∆APB vuông vì có góc vuông (góc nội tiếp chắn nửa cung tròn)
Tứ giác AOPM nội tiếp đường tròn vì có +
= 2v. Nên
=
(cùng chắn cung OP).
Vậy hai tam giác vuông MON à APB đồng dạng vị có cắp góc nhọn bằng nhau.
b)
Tam giác AM = MP, BN = NP (1) (tính chất hai tiếp tuyến cắt nhau)
Tam giác vuông MON có OP là đường cao nên:
MN.PN = OP2 (2)
Từ 1 và 2 suy ra AM.BN = OP2 = R2
c) Từ tam giác MON đồng dạng với tam giác APB ta có :
Khi AM = thi do AM.BN = R2 suy ra BN = 2R
Do đó MN = MP + PN = AM + BN = + 2R =
Suy ra MN2 =
Vậy =
d) Nửa hình tròn APB quay quanh bán kính AB = 2R sinh ra một hình cầu có bán kính R.
Vậy V = πR3

Em kham khảo link này nhé.
Câu hỏi của Trần Đức Thắng - Toán lớp 9 - Học toán với OnlineMath