Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

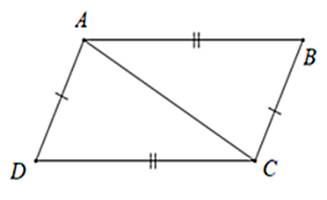
a)Xét \(\Delta ABD\) và \(\Delta CDB\) có:
AB=CD (gt)
\(\widehat {ABD} = \widehat {CDB}\) (gt)
BD chung
Vậy \(\Delta ABD = \Delta CDB\)(c.g.c)
b)Xét \(\Delta OAD\) và \(\Delta OCB\) có:
AO=CO (gt)
\(\widehat {AOD} = \widehat {COB}\) (đối đỉnh)
OD=OB (gt)
Vậy \(\Delta OAD = \Delta OCB\)(c.g.c)

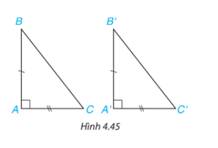
Xét 2 tam giác ABC và A’B’C có:
AB=A’B’ (gt)
\(\widehat A = \widehat {A'}\) (gt)
AC=A’C’ (gt)
\( \Rightarrow \Delta ABC = \Delta A'B'C'\)(c.g.c)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 13 và cho biết chúng bằng nhau theo trường hợp nào.
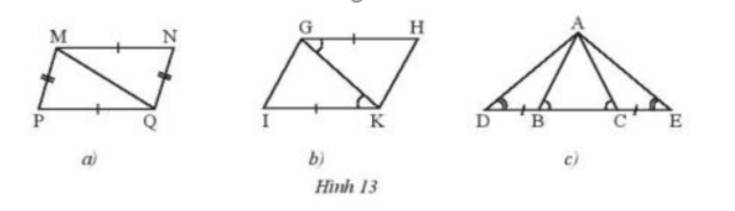

a) Ta thấy tam giác MNQ = tam giác MPQ (c-c-c)
b) Ta thấy tam giác GHK = tam giác GIK (c-g-c)
c) Ta thấy tam giác ADB = tam giác ACE (g-c-g)
Tam giác ADC = tam giác AEB (g-c-g)
Hãy chỉ ra các cặp tam giác bằng nhau trong Hình 22 và cho biết chúng bằng nhau theo trường hợp nào.
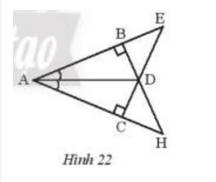

+) Xét \(\Delta{ABD}\) vuông tại B và \(\Delta{ACD}\) vuông tại D có:
AD chung
\(\widehat {BAD} = \widehat {DAC}\) (gt)
\( \Rightarrow \Delta{ABD}=\Delta{ACD}\) (cạnh huyền – góc nhọn)
\( \Rightarrow \) BD = CD, AB = AC ( 2 cạnh tương ứng)
\( \widehat {BDA} = \widehat {ADC}\)( 2 góc tương ứng)
+) Xét \(\Delta{BED}\) vuông tại B và \(\Delta{CHD}\) vuông tại C có:
BD = CD (cmt)
\(\widehat {BDE} = \widehat {CDH}\)( 2 góc đối đỉnh )
\( \Rightarrow \Delta{BED}=\Delta{CHD \) (cạnh góc vuông - góc nhọn kề )
+) Ta có: \(\widehat {BDA} + \widehat {BDE}\)= \(\widehat {ADE}\)
\(\widehat {ADC} + \widehat {CDH}\)= \(\widehat {ADH}\)
Mà \(\widehat {BDA} = \widehat {ADC}\), \(\widehat {BDE} = \widehat {CDH}\)
\( \Rightarrow \widehat {ADE} = \widehat {ADH}\)
Xét \(\Delta{ADE}\) và \(\Delta{ADH}\) có:
\(\widehat {BAD} = \widehat {DAC}\) (gt)
AD chung
\(\widehat {ADE} = \widehat {ADH}\) (cmt)
\( \Rightarrow \Delta{ADE}=\Delta{ADH}\)( g – c – g )
+) Xét \(\Delta{ABH}\) vuông tại B và \(\Delta{ACE}\) vuông tại C có:
AB = AC (cmt)
\(\widehat {BAH}\) chung
\( \Rightarrow \Delta{ABH}=\Delta{ACE}\) (cạnh góc vuông – góc nhọn kề)

Bạn tự vẽ hình nhé
Xét tứ giác EHDA có 3 góc vuông ( CAB = HDA = EHD = 90 độ ) nên AHDA là hình chữ nhật
b) HE song song với AC do cùng vuông với AB
HD song song với AB do cùng vuông với AC
c) Do EHDA là hình chữ nhật nên góc HEA = 90 độ và góc HDA = 90 độ
suy ra góc BEH = góc HDC = 90 độ
Do EH song song với AC nên góc BHE = góc C ( hai góc đồng vị )
Do HD song song với AB nên gocsDHC = góc C ( hai góc đồng vị )
d) Ta thấy: góc BHE + góc EHA = góc BHA = 90 độ ( do H vuông góc với BC )
góc DHA + góc EHA = góc EHD = 90 độ ( do HE vuông góc HD )
suy ra góc BHE = góc DHA
Tương tự ta có góc EHA = góc DHC ( cùng phụ với góc AHD )
e) Ta thấy góc BAH + góc HAC = 90 độ
góc ACB + góc HAC = 180 độ - góc AHC = 90 độ
Suy ra góc BAH = góc ACB
Đây là lời giải chi tiết đó bạn

+)Xét hai tam giác vuông ABC và XYZ có:
\(\widehat A = \widehat X( = 90^\circ )\) (gt)
AC=XZ (gt)
\(\widehat C = \widehat Z\) (gt)
\( \Rightarrow \Delta ABC = \Delta XYZ\) (g.c.g)
+)Xét hai tam giác vuông DEF và GHK có:
\(EF = HK\) (gt)
\(\widehat {EFD} = \widehat {GKH}\) (gt)
\( \Rightarrow \Delta DEF = \Delta GHK\) (cạnh huyền – góc nhọn)
+)Xét hai tam giác vuông MNP và RTS có:
\(MN = TR\) (gt)
\(\widehat R = \widehat M( = 90^\circ )\) (gt)
\(PM = SR\) (gt)
\( \Rightarrow \Delta MNP = \Delta RTS\) (c.g.c)