Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{a}+\overrightarrow{b}+3\overrightarrow{c}=\overrightarrow{0}\Leftrightarrow\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}=-2\overrightarrow{c}\)
\(\Leftrightarrow\left(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\right)^2=\left(-2\overrightarrow{c}\right)^2\)
\(\Leftrightarrow\overrightarrow{a}^2+\overrightarrow{b}^2+\overrightarrow{c}^2+2\left(\overrightarrow{a}.\overrightarrow{b}+\overrightarrow{b}.\overrightarrow{c}+\overrightarrow{c}.\overrightarrow{a}\right)=4\overrightarrow{c}^2\)
\(\Leftrightarrow A=\dfrac{4x^2-\left(x^2+y^2+z^2\right)}{2}=\dfrac{3x^2-y^2-z^2}{2}\)

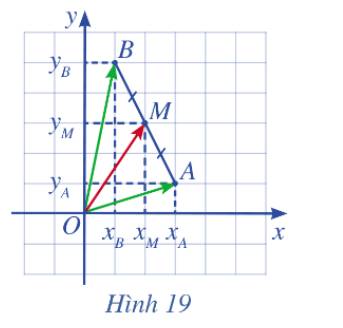
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

\(\overrightarrow{AB}=\overrightarrow{AG}+\overrightarrow{GB}=\overrightarrow{b}-\overrightarrow{a}\)
\(\overrightarrow{GC}=0-\overrightarrow{GA}-\overrightarrow{GB}=-\overrightarrow{a}-\overrightarrow{b}\)
\(\overrightarrow{BC}=\overrightarrow{BG}+\overrightarrow{GC}=-\overrightarrow{b}-\overrightarrow{a}-\overrightarrow{b}=-\overrightarrow{a}-2\overrightarrow{b}\)
\(\overrightarrow{CA}=\overrightarrow{CG}+\overrightarrow{GA}=\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{a}=2\overrightarrow{a}+\overrightarrow{b}\)

Cách 1:
Gọi O là giao điểm của AC và BD.

Ta có:
\(\begin{array}{l}\overrightarrow {AG} = \overrightarrow {AB} + \overrightarrow {BG} = \overrightarrow a + \overrightarrow {BG} ;\\\overrightarrow {CG} = \overrightarrow {CB} + \overrightarrow {BG} = \overrightarrow {DA} + \overrightarrow {BG} = - \overrightarrow b + \overrightarrow {BG} ;\end{array}\)(*)
Lại có: \(\overrightarrow {BD} =\overrightarrow {BA} + \overrightarrow {AD} = - \overrightarrow a + \overrightarrow b \).
\(\overrightarrow {BG} ,\overrightarrow {BD} \) cùng phương và \(\left| {\overrightarrow {BG} } \right| = \frac{2}{3}BO = \frac{1}{3}\left| {\overrightarrow {BD} } \right|\)
\( \Rightarrow \overrightarrow {BG} = \frac{1}{3}\overrightarrow {BD} = \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right)\)
Do đó (*) \( \Leftrightarrow \left\{ \begin{array}{l}\overrightarrow {AG} = \overrightarrow a + \overrightarrow {BG} = \overrightarrow a + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\\\overrightarrow {CG} = -\overrightarrow b + \overrightarrow {BG} = -\overrightarrow b + \frac{1}{3}\left( { - \overrightarrow a + \overrightarrow b } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b ;\end{array} \right.\)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)
Cách 2:
Gọi AE, CF là các trung tuyến trong tam giác ABC.
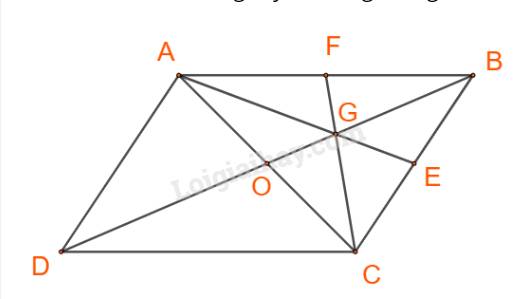
Ta có:
\(\overrightarrow {AG} = \frac{2}{3}\overrightarrow {AE} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {AB} + \overrightarrow {AC} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\overrightarrow {AB} + \left( {\overrightarrow {AB} + \overrightarrow {AD} } \right)} \right] \\= \frac{1}{3}\left( {2\overrightarrow a + \overrightarrow b } \right) = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
\(\overrightarrow {CG} = \frac{2}{3}\overrightarrow {CF} = \frac{2}{3}.\frac{1}{2}\left( {\overrightarrow {CA} + \overrightarrow {CB} } \right) = \frac{2}{3}.\frac{1}{2}\left[ {\left( {\overrightarrow {CB} + \overrightarrow {CD} } \right) + \overrightarrow {CB} } \right] = \frac{1}{3}\left( {2\overrightarrow {CB} + \overrightarrow {CD} } \right) = \frac{1}{3}\left( { - 2\overrightarrow {AD} - \overrightarrow {AB} } \right) = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b \)
Vậy \(\overrightarrow {AG} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b ;\;\overrightarrow {CG} = - \frac{1}{3}\overrightarrow a - \frac{2}{3}\overrightarrow b .\)


Bước 1: Dựng hình bình hành có cạnh song song với giá của vecto \(\overrightarrow a ,\;\overrightarrow b \) và đường chéo là vecto \(\overrightarrow u ,\;\overrightarrow v \).
Ta dựng được hình hình hành ABCD và DEGH. Trong đó: DC và DE nằm trên giá của vecto \(\overrightarrow a \), DA và DH nằm trên giá của vecto \(\overrightarrow b \), còn vecto \(\overrightarrow u ,\;\overrightarrow v \) lần lượt là hai dường chéo.
Dễ thấy: \(\overrightarrow u = \overrightarrow {DA} + \overrightarrow {DC} ,\;\overrightarrow v = \overrightarrow {DH} + \overrightarrow {DE} \)
Mà \(\overrightarrow {DA} = 3\overrightarrow b ,\;\overrightarrow {DC} = \overrightarrow a \;,\;\overrightarrow {DH} = 3\overrightarrow b ,\;\overrightarrow {DE} = - 2\overrightarrow a .\)
\( \Rightarrow \overrightarrow u = 2\overrightarrow b + \overrightarrow a ,\;\,\overrightarrow v = 3\overrightarrow b - 2\overrightarrow a \)