Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Công thức tổng quát số đo của góc lượng giác \(\left(Ox,ON\right)=70^o+k\cdot360,k\in Z\)
Công thức tổng quát số đo của lượng giác
\(\left(Ox,OP\right)=\left(Ox,OM\right)+\left(OM,OP\right)=-50-120^o+m\cdot360^o=-170^o+m\cdot360^o,m\in Z\)

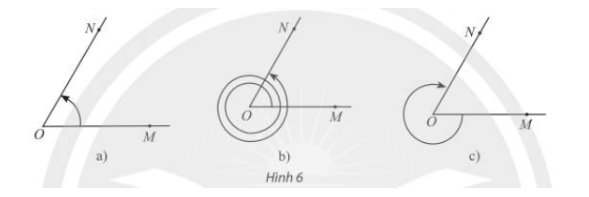
a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)
b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)
c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)
Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)

Ta có: \(\left(OA,OM\right)=120^o+k\cdot360^o,k\in Z\\ \left(OA,ON\right)=-75^o+k\cdot360^o,k\in Z\)

a) Ta có: \({u_1} = 1,{u_2} = 2,{u_3} = 3\)
Dự đoán \({u_n} = n\)
b) Ta có: \(\begin{array}{l}{v_1} = 1\\{v_2} = 8 = {2^3}\\{v_3} = 27 = {3^3}\\{v_4} = 64 = {4^3}\end{array}\)
Dự đoán: \({v_n} = {n^3}\)

a. Năm số hạng đầu của dãy số
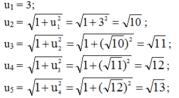
b. Dự đoán công thức số hạng tổng quát của dãy số:
un =√(n+8) (1)
Rõ ràng (1) đúng với n = 1
Giả sử (1) đúng với n = k, nghĩa là uk = √(k+8)
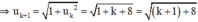
⇒ (1) đúng với n = k + 1
⇒ (1) đúng với mọi n ∈ N*.

a) Công thức tính giá trị của ô tô:
- Sau 1 năm: \(800 - 800.4\% = 768\) (triệu đồng)
- Sau 2 năm: \(768 - 768.4\% = 737,28\) (triệu đồng)
b) Công thức tính giá trị của ô tô sau n năm sử dụng: \({S_n} = 800{\left( {1 - 0,04} \right)^n}\)
c) Sau 10 năm, giá trị của ô tô ước tính còn: \({S_{10}} = 800{\left( {1 - 0,04} \right)^{10}} \approx 531,87\) (triệu đồng)
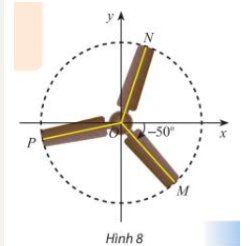


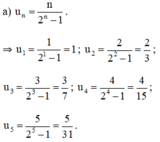
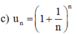
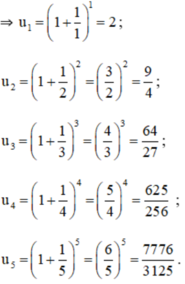
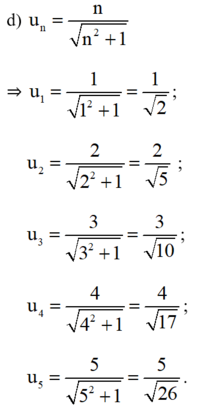
Vì mâm bánh xe ô tô được chia thành năm phần bằng nhau nên mỗi phần có số đo bằng \(\dfrac{360^o}{5}=72^o\)
Ta có: \(\left(ON,OM\right)=\left(ON,Ox\right)+\left(Ox,OM\right)\\ \Rightarrow\left(ON,Ox\right)=99^o\)
Công thức số đo tổng quát của góc lượng giác \(\left(ON,Ox\right)=99^o+k\cdot360^o,k\in Z\)