Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: MBM'C' là hình bình hành nên C'M // BM'
Mà BM' thuộc (A'BM')
Suy ra: C'M // (A'BM')
b) △A'BM' có: \(\dfrac{A'K}{A'B}=\dfrac{A'G'}{A'M'}=\dfrac{2}{3}\)
Nên G'K // BM' mà BM' thuộc (BCC'B')
Suy ra: G'K // (BCC'B')
c) Hình bình hành AMM'A' có: GG' // MM'
Mà MM' thuộc (BCC'B')
Suy ra: GG' // (BCC'B')
Mà G'K // (BCC'B')
Do đó: (GG'K) // (BCC'B')
d) Trong mp(ABB’A’), vẽ đường thẳng qua K và song song với AB, A’B’; cắt A’A và B’B lần lượt tại J và H.
Trong mp (ACC’A”), vẽ đường thẳng qua J và song song với AC, A’C’; cắt C’C tại I.
Ta có: IJ // AC mà AC ⊂ (ABC) nên IJ // (ABC);
JK // AB mà AB ⊂ (ABC) nên JK // (ABC).
Lại có IJ và JK cắt nhau tại J và cùng nằm trong mp(IJK) nên (IJK) // (ABC).
Theo bài, mp(α) // (ABC) và đi qua K nên mp(α) chính là mp(IJK).
Khi đó CC’ cắt (α) tại I.
Ta có: (IJK) // (ABC) mà (ABC) // (A’B’C’) nên (A’B’C’), (IJK), (ABC) là ba mặt phẳng song song với nhau.

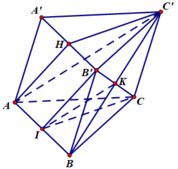
Gọi K là giao điểm của B’C và BC’, I là trung điểm của AB.
Do HB’= AI và HB’ //AI nên AHB’I là hình bình hành
=> AH// B’I.
Mặt khác : KI// AC’ nên (AHC’) // (B’CI).
Do đó: B’C //(AHC’).
Chọn A.

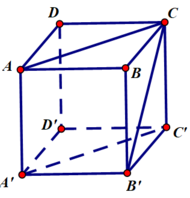
a) Góc giữa AB và B’C’ = góc giữa AB và BC (vì B’C’//BC)
⇒ Góc giữa AB và B’C’ = A B C ^ = 90 o
b) Góc giữa AC và B’C’ = góc giữa AC và BC (vì B’C’//BC)
⇒ Góc giữa AC và B’C’ = A C B ^ = 45 o
c) Góc giữa A’C’ và B’C = góc giữa AC và B’C (vì A’C’//AC)
ΔACB’ đều vì AC = B’C = AB’ (đường chéo của các hình vuông bằng nhau)
⇒ Góc giữa A’C’ và B’C = A C B ' ^ = 60 o

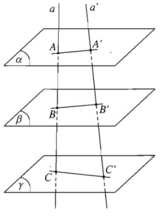
Vì (α) // (β) // (γ) nên
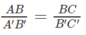
Mặt khác ta có:
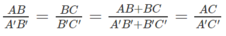
Suy ra:
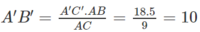
Vậy A’B’ = 10 và
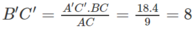
Vậy B’C’ = 8.

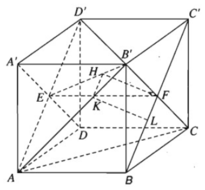
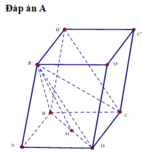
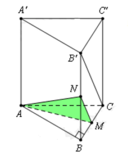
a) Ta có B'C ⊥ BC' vì đây là hai đường chéo của hình vuông BB'C'C
Ngoài ra ta còn có: A'B' ⊥ (BB'C'C) ⇒ A'B' ⊥ BC'
Từ đó ta suy ra BC' ⊥ (A'B'CD) vì mặt phẳng (A'B'CD) chứa đường thẳng A'B' và B'C cùng vuông góc với BC'.
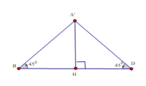
b) Mặt phẳng (AB'D') chứa đường thẳng AB' và song song với BC', ta hãy tìm hình chiếu của BC' trên mặt phẳng (AB'D'). Gọi E, F lần lượt là tâm các hình vuông ADD'A', BCC'B'. Kẻ FH ⊥ EB'với H ∈ EB', khi đó FH nằm trên mặt phẳng (A'B'CD) nên theo câu a) thì FH ⊥ (AB'D'), do đó hình chiếu BC' trên mặt phẳng (AB'D) là đường thẳng đi qua H và song song với BC'. Giả sử đường thẳng đó cắt AB' tại K thì từ K vẽ đường thẳng song song với FH cắt BC' tại L. Khi đó KL là đoạn vuông góc chung cần dựng. Tam giác B'EF vuông tại F nên từ công thức
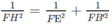
ta tính được
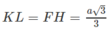
Nhận xét . Độ dài đoạn vuông góc chung của AB' và BC' bằng khoảng cách giữa hai mặt phẳng song song (AB'D') và (BC'D) lần lượt chứa hai đường thẳng đó.
Khoảng cách này bằng 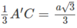
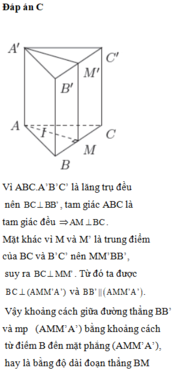
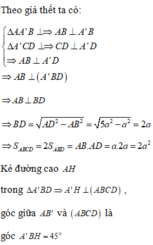

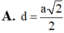
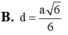
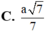
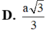

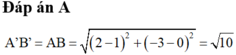
Áp dụng định lí Thales cho ba mặt phẳng đôi một song song (P), (Q), (R) và hai cát tuyến d, d' ta có:
\(\frac{{AB}}{{BC}} = \frac{{A'B'}}{{B'C'}}\) suy ra \(\frac{2}{4} = \frac{3}{{B'C'}}\)
=> B'C' = 6 (cm).