Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Mỗi hình vuông là một hình thoi (có một góc vuông). Vậy A ⊂ B, A ≠ B.
b) Mỗi số là ước của 6 là một ước chung của 24 và 30.
n ∈ B => n ∈ A. Vậy B ⊂ A. Mặt khác mỗi ước chung của 24 và 30 là một ước của 6. Vậy A ⊂ B. Suy ra A= B.
a) Mỗi hình vuông là một hình thoi (có một góc vuông). Vậy A ⊂ B, A ≠ B.
b) Mỗi số là ước của 6 là một ước chung của 24 và 30.
n ∈ B => n ∈ A. Vậy B ⊂ A. Mặt khác mỗi ước chung của 24 và 30 là một ước của 6. Vậy A ⊂ B. Suy ra A= B.

a) \(A = \{ x \in \mathbb{N}|\;x < 2\} = \{ 0;1\} \) và \(B = \{ x \in \mathbb{R}|\;{x^2} - x = 0\} = \{ 0;1\} \)
Vậy A = B, A là tập con của tập B và ngược lại.
b) D là tập hợp con của C vì: Mỗi hình vuông đều là một hình thoi đặc biệt: hình thoi có một góc vuông.
\(C \ne D\) vì có nhiều hình thoi không là hình vuông, chẳng hạn:
c) \(E = ( - 1;1] = \left\{ {x \in \mathbb{R}|\; - 1 < x \le 1} \right\}\) và \(F = ( - \infty ;2] = \left\{ {x \in \mathbb{R}|\;x \le 2} \right\}\)
E là tập con của F vì \( - 1 < x \le 1 \Rightarrow x \le 2\) .
\(E \ne F\) vì \( - 3 \in F\)nhưng \( - 3 \notin E\)

A = {n ∈ N | n là một ước chung của 24 và 30} = {1; 2; 3; 6}.
B = {n ∈ N | n là một ước của 6} = {1; 2; 3; 6}.
Ta thấy A ⊂ B và B ⊂ A nên A = B.

a) A là tập con củ B vì:
\( - \sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( { - \sqrt 3 } \right)^2} - 3 = 0\), nên \( - \sqrt 3 \in B\)
\(\sqrt 3 \in \mathbb{R}\) thỏa mãn \({\left( {\sqrt 3 } \right)^2} - 3 = 0\), nên \(\sqrt 3 \in B\)
Lại có: \({x^2} - 3 = 0 \Leftrightarrow x = \pm \sqrt 3 \) nên \(B = \{ - \sqrt 3 ;\sqrt 3 \} \).
Vậy A = B.
b) C là tập hợp con của D vì: Mỗi tam giác đều đều là một tam giác cân.
\(C \ne D\) vì có nhiều tam giác cân không là tam giác đều, chẳng hạn: tam giác vuông cân.
c) E là tập con của F vì \(24\; \vdots \;12\) nên các ước nguyên dương của 12 đều là ước nguyên dương của 24.
\(E \ne F\) vì \(24 \in F\)nhưng \(24 \notin E\)

Tham khảo:
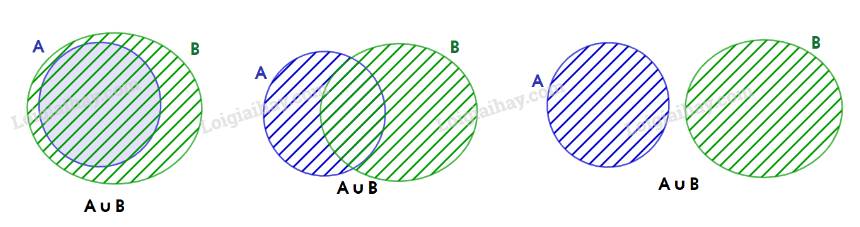
a) \(A \subset A \cup B\) vì
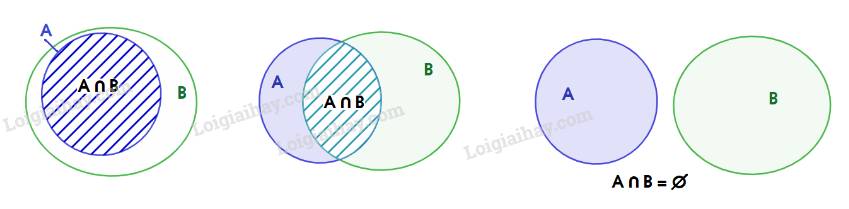
b) \(A \cap B \subset A\) vì

Để xác định xem tập hợp A có phải là tập con của tập hợp B hay không, ta cần kiểm tra xem tất cả các phần tử trong tập hợp A có thuộc tập hợp B hay không. Tương tự, để xác định xem tập hợp B có phải là tập con của tập hợp A hay không, ta cần kiểm tra xem tất cả các phần tử trong tập hợp B có thuộc tập hợp A hay không.
Tập hợp A được xác định bởi điều kiện (x-1)(x-2)(x-4)=0. Điều này có nghĩa là các giá trị của x mà khi thay vào biểu thức (x-1)(x-2)(x-4) thì biểu thức này sẽ bằng 0. Các giá trị này là 1, 2 và 4. Do đó, tập hợp A là {1, 2, 4}.
Tập hợp B được xác định bởi các ước của số 4. Số 4 có các ước là 1, 2 và 4. Do đó, tập hợp B cũng là {1, 2, 4}.
Vì tập hợp A và tập hợp B đều chứa các phần tử 1, 2 và 4, nên ta có thể kết luận rằng tập hợp A là tập con của tập hợp B và tập hợp B là tập con của tập hợp A.
Vậy, tập hợp A và tập hợp B là bằng nhau.
Vì mỗi hình vuông đều là một hình thoi nên A ⊂ B.
Có những hình thoi không phải là hình vuông nên B ⊄ A.
Vậy A ≠ B.