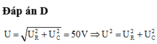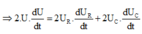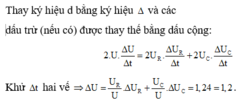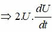Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng

Bài này thì có vẹo gì đâu bạn.
\(u=100\sqrt 2\cos(100\pi t)(V)\)
\(Z_L=\omega L = 10\Omega\)
\(Z_C=\dfrac{1}{\omega C}=20\Omega\)
Tổng trở \(Z=\sqrt{r^2+(Z_L-Z_C)^2}=10\sqrt 2 \Omega\)
\(\Rightarrow I_o=\dfrac{U_0}{Z}=10A\)
\(\tan\varphi=\dfrac{Z_L-Z_C}{R}=-1\Rightarrow \varphi=-\dfrac{\pi}{4}\)
Suy ra: \(\varphi=\dfrac{\pi}{4}\)
Vậy \(i=10\cos(100\pi t +\dfrac{\pi}{4})\) (A)

Đáp án D
U = U R 2 + U C 2 = 50 V ⇒ U 2 = U R 2 + U C 2 ⇒ 2 . U . d U d t = 2 U R . d U R d t + 2 U C . d U C d t
Thay ký hiệu d bằng ký hiệu ∆ và các dấu trừ (nếu có) được thay thế bằng dấu cộng:
2 . U . ∆ U ∆ t = 2 U R . ∆ U R ∆ t + 2 U C . ∆ U C ∆ t
Khử ∆ t hai vế
⇒ ∆ U = U R U . ∆ U R + U C U . ∆ U C = 1 , 24 = 1 , 2
⇒ U = 50 ± 1,2V

Giải thích: Đáp án C
Từ biểu thức ![]()
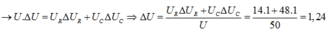
Do đó: ![]()
v Cách tính sai số của một biểu thức bất kì
*Biểu thức có dạng tích và thương. 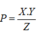
Bước 1: Lấy ln hai vế ta được ![]()
Bước 2: Thay x’=∆x và đổi dấu âm thành dương.
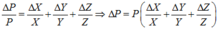
*Biểu thức có chứa dạng mũ dưới dạng tổng hoặc hiệu thì bước đầu tiên ta tiến hành đạo hàm hai vế để hạ thấp số mũ. Sau đó thực hiện các bước như trên.