Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để đặt mật khẩu ta thực hiện 3 hành động liên tiếp: chọn chữ số hàng trăm, chọn chữ số hàng chục, chọn chữ số hàng đơn vị.
Chọn chữ số hàng trăm: Có 4 cách chọn.
Chọn chữ số hàng chục: Có 4 cách chọn.
Chọn chữ số hàng đơn vị: Có 4 cách chọn.
Vậy có 4.4.4=64 cách đặt mật khẩu.

a) Mỗi kí tự đều có 10 cách chọn.
Số mật khẩu có thể tạo ra là 10. 10. 10 = 1000
b) - Kí tự đầu có 26 cách chọn.
- 2 kí tự sau, mỗi kí tự có 10 cách chọn.
Quy định mới có thể tạo ra số mật khẩu là:
26. 10. 10 = 2600
Quy định mới có thể tạo được nhiều hơn quy định cũ số mật khẩu khác nhau là:
2600 - 1000= 1600 (mật khẩu)

Tham khảo:
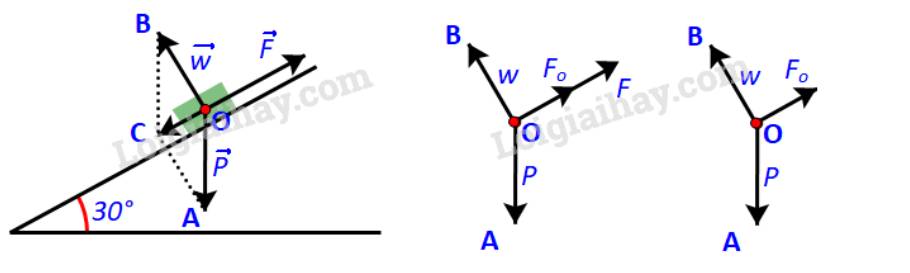
Khẩu pháo chịu tác động của ba lực: trọng lực \(\overrightarrow P \)(kí hiệu \(\overrightarrow {OA} \)), phản lực \(\overrightarrow w \)(kí hiệu \(\overrightarrow {OB} \)) và lực kéo \(\overrightarrow F \). Để kéo pháo thì độ lớn của lực kéo phải lớn hơn độ lớn của lực kéo khi pháo cân bằng \(\overrightarrow {{F_o}} \)(kí hiệu \(\overrightarrow {O{F_o}} \) )
Khi pháo cân bằng thì: \(\overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow 0 \)
Để tổng hợp lực \(\overrightarrow P \) và \(\overrightarrow w \), ta vẽ hình bình hành OACB.
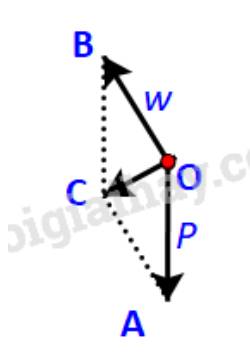
Ta có:
\(OB = \;AC;\;\;OB//\;AC\;\; \Rightarrow \overrightarrow {OB} = \;\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {OB} + \overrightarrow {OA} = \overrightarrow {AC} + \overrightarrow {OA} = \overrightarrow {OA} + \overrightarrow {AC} = \overrightarrow {OC} \)
\( \Rightarrow \overrightarrow 0 = \overrightarrow P + \overrightarrow w + \overrightarrow {{F_o}} = \overrightarrow {OB} + \overrightarrow {OA} + \overrightarrow {O{F_o}} = \overrightarrow {OC} + \overrightarrow {O{F_o}} \)
\( \Rightarrow \;O\) là trung điểm của \(C{F_o}\), hay \(OC = \left| {\overrightarrow {{F_o}} } \right|\).
Lại có: \(OB \bot \;\;OC\)(do \(\overrightarrow {OB} \) là phản lực)
\( \Rightarrow \;AC \bot CO \Rightarrow OC = OA\,.\,\,\cos \widehat {AOC}\)
Mà \(\widehat {AOC} = {90^o} - {30^o} = {60^o}\); \(\left| {\overrightarrow P } \right| = OA = 22\;148\;N\)
\( \Rightarrow OC = 22\;148\,.\,\,\cos {60^o} = 11074\;\left( N \right)\)
Vậy lực \(\overrightarrow {{F_o}} \)có độ lớn là \(11\;074\;N\), để kéo pháo thì lực \(\overrightarrow F \) cùng hướng với \(\overrightarrow {{F_o}} \) và \(\left| {\overrightarrow F } \right| > 11\;074\;N\)
Vì \(11\;074\;:100 = 110,74\) nên cần tối thiểu 111 người để kéo pháo.

a) Máy bay đến sân bay Đà Nẵng ứng với thời gian t (giờ) thỏa mãn:
\(\left\{ \begin{array}{l}16,1 = 21,2 - \frac{{153}}{{40}}t\\108,2 = 105,8 + \frac{9}{5}t\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{{153}}{{40}}t = 5,1\\\frac{9}{5}t = 2,4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}t = \frac{4}{3}\\t = \frac{4}{3}\end{array} \right. \Leftrightarrow t = \frac{4}{3}\).
Chuyến bay từ Hà Nội đến Đà Nẵng mất \(\frac{4}{3}\) giờ.
b) Tại thời điểm \(t = 1\) giờ, ta có \(x = 21,2 - \frac{{153}}{{40}}.1 = 17,375\)
Vậy tại thời điểm 1 giờ sau khi cất cánh , máy bay ở vị trí có vĩ độ \(17,{375^o}\) Bắc nên máy bay đã bay qua vĩ tuyến 17.

+) Số cách chọn 4 kí tự đầu tiên là: \(A_{10}^4\) (cách chọn)
+) Số cách chọn 2 kí tự tiếp theo là: \(C_{26}^1.C_{26}^1\) (cách chọn)
+) Số cách chọn 1 kí tự tiếp theo là: \(C_{26}^1\) (cách chọn)
+) Số cách chọn 1 kí tự cuối cùng là: \(C_{10}^1\) (cách chọn)
+) Áp dụng quy tắc nhân, ta có số mật khẩu có thể tạo thành là:
\(A_{10}^4.C_{26}^1.C_{26}^1.C_{26}^1.C_{10}^1\) ( mật khẩu)

a) (E) có tiêu điểm \({F_1}\left( { - \sqrt 3 ;0} \right)\) nên \(c = \sqrt 3\).
Phương trình chính tăc của (E) có dạng
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\)
Ta có: \(M\left( {1;{{\sqrt 3 } \over 2}} \right) \in (E)\)
\(\Rightarrow {1 \over {{a^2}}} + {3 \over {4{b^2}}} = 1\ (1)\)
Và \({a^2} = {b^2} + {c^2} = {b^2} + 3\)
Thay vào (1) ta được :
\(\eqalign{ & {1 \over {{b^2} + 3}} + {3 \over {4{b^2}}} = 1 \cr & \Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^2}(b + 3) \cr}\)
\(\Leftrightarrow 4{b^4} + 5{b^2} - 9 = 0 \Leftrightarrow {b^2} = 1\)
Suy ra \({a^2} = 4\)
Ta có a = 2 ; b = 1.
Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0)
(0 ; -1) và (0 ; 1).
b) Phương trình chính tắc của (E) là :
\({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)
c) (E) có tiêu điểm thứ hai là điểm \(\left( {\sqrt 3 ;0} \right)\). Đường thẳng \(\Delta\) đi qua điểm\(\left( {\sqrt 3 ;0} \right)\) và vuông góc với Ox có phương trình \(x = \sqrt 3\).
Phương trình tung độ giao điểm của \(\Delta\) và \((E)\) là :
\({3 \over 4} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = \pm {1 \over 2}\)
Suy ra tọa độ của C và D là :
\(C\left( {\sqrt 3 ; - {1 \over 2}} \right)\) và \(\left( {\sqrt 3 ;{1 \over 2}} \right)\)
Vậy CD = 1.