Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

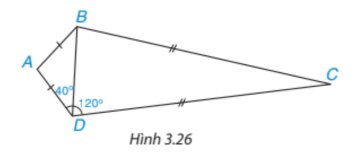
* Xét tam giác ABD cân tại A (vì AB = AD) ta có:
• \(\widehat {AB{\rm{D}}} = \widehat {A{\rm{D}}B} = {40^o}\)
• \(\widehat A + \widehat {AB{\rm{D}}} + \widehat {A{\rm{D}}B} = {180^o}\)
Suy ra \(\widehat A\)=180°−\(\widehat {AB{\rm{D}}}\)−\(\widehat {A{\rm{D}}B}\)=180°−40°−40°=100°
Ta có \(\widehat {A{\rm{D}}B} + \widehat {B{\rm{D}}C}\)=120° suy ra \(\widehat {B{\rm{D}}C}\)=120°−\(\widehat {A{\rm{D}}B}\)=120°−40°=80°.
* Xét tam giác BCD cân tại C (vì BC = CD) ta có:
• \(\widehat {CB{\rm{D}}} = \widehat {C{\rm{D}}B}\)=80°
• \(\widehat C + \widehat {CB{\rm{D}}} + \widehat {C{\rm{D}}B}\)=180°
Suy ra \(\widehat C\)=180°−\(\widehat {CB{\rm{D}}} - \widehat {C{\rm{D}}B}\)=180°−80°−80°=20°
Ta có: \(\widehat {ABC} = \widehat {AB{\rm{D}}} + \widehat {CB{\rm{D}}}\)=40°+80°=120o
Vậy số đo các góc của tứ giác ABCD là \(\widehat A = {100^o};\widehat {ABC} = {120^o};\widehat C = {20^o}\)

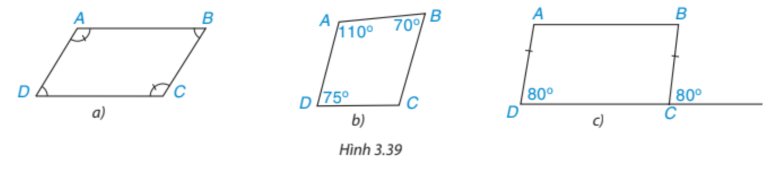
* Hình 3.39a)
Tứ giác ABCD có: \(\widehat A = \widehat C;\widehat B = \widehat D \)
Do đó, tứ giác ABCD là hình bình hành.
* Hình 3.39b)
Tứ giác ABCD có: \(\widehat B \ne \widehat D\) (70°≠75°).
Do đó, tứ giác ABCD không là hình bình hành.
* Hình 3.39c)
Đặt \(\widehat {BC{\rm{x}}} = {80^o}\) (như hình vẽ)
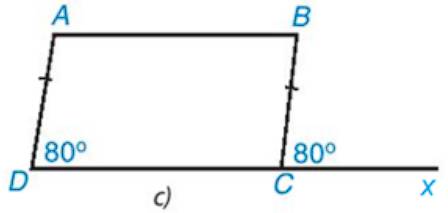
Ta có: \(\widehat D = \widehat {BC{\rm{x}}} = {80^o}\) mà hai góc này ở vị trí đồng vị nên AD // BC.
Tứ giác ABCD có:
• AD // BC (chứng minh trên)
• AD = BC (giả thiết)
Do đó, tứ giác ABCD là hình bình hành.
Vậy tứ giác ABCD trong Hình 3.39a) và 3.39c) là hình bình hành; tứ giác ABCD trong Hình 3.39b) không là hình bình hành.

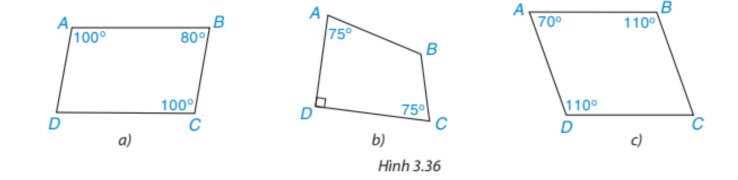
* Hình 3.36a)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
100°+80°+100°+\(\widehat D = {360^o}\)
280°+\(\widehat D\)=360°
Suy ra \(\widehat D\)=360°−280°=80°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=100°; \(\widehat B = \widehat D\)=80°
Do đó, tứ giác ABCD là hình bình hành.
* Hình 3.36b)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
75°+\(\widehat B\)+75°+90°=360°
240°+\(\widehat B\)=360°
Suy ra \(\widehat B\)=360°−240°=120°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=100° nhưng \(\widehat B \ne \widehat D\)(120°≠90°)
Do đó, tứ giác ABCD không là hình bình hành.
* Hình 3.36c)
Xét tứ giác ABCD có: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
70°+110°+\(\widehat C\)+110°=360°
\(\widehat C\)+290°=360o
Suy ra \(\widehat C\)=360°−290°=70°
Tứ giác ABCD có: \(\widehat A = \widehat C\)=70°; \(\widehat B = \widehat D\)=110°
Do đó, tứ giác ABCD là hình bình hành.
Vậy tứ giác ABCD trong Hình 3.36a) và 3.36c) là hình bình hành; tứ giác ABCD trong Hình 3.36b) không là hình bình hành.


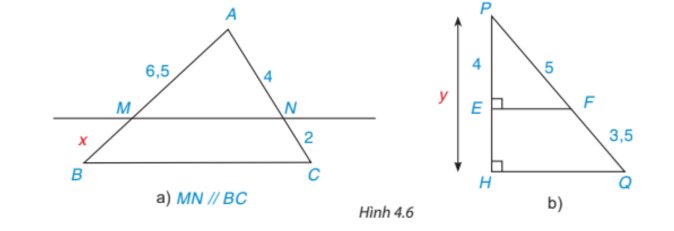
a)
Xét tam giác ABC có MN//BC
`=>(AM)/MB=(AN)/(NC)` (định lí thales)
`=>(6,5)/x=4/2`
`=>x=3,25`
b)
có QH⊥PH (hình vẽ)
FE⊥PH (hình vẽ)
Suy ra EF//HQ (từ vuông góc đến song song)
Xét tam giác PHQ có EF//HQ (cmt)
`=>(PE)/(PH)=(PF)/(PQ)` (định lí thales)
`=>4/x=5/(5+3,5)`
`=>4/x=5/(8,5)`
`=>x=6,8`

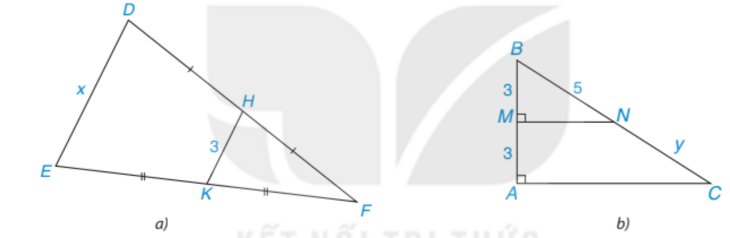
a. Do H, K lần lượt là trung điểm cạnh DF, EF
⇒ HK là đường trung bình của tam giác DEF.
⇒ DE = 2 HK = 2 \(\times\) 3 = 6.
b. Do M là trung điểm cạnh AB mà MN // AC (cùng vuông góc với AB)
⇒ MN là đường trung bình của tam giác ABC.
⇒ N là trung điểm của cạnh BC
⇒ y = NB = NC = 5.

Tứ giác ABCD là hình bình hành vì hai cạnh đối AD, BC song song và bằng nhau.
Tứ giác IKMN là hình bình hành vì KM // IN, IK // MN (hoặc vì \(\widehat{I}=\widehat{M},\widehat{K}=\widehat{N}\) )
Tứ giác ABCD là hình bình hành
Tứ giác IKMN là hình bình hành

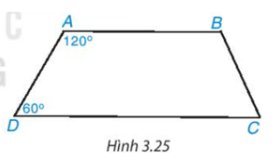
Do \(\widehat{A}+\widehat{D}=120^o+60^o=180^o\)
\(\Rightarrow AB//CD\)
\(\Rightarrow\) ABCD là hình thang.

Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.
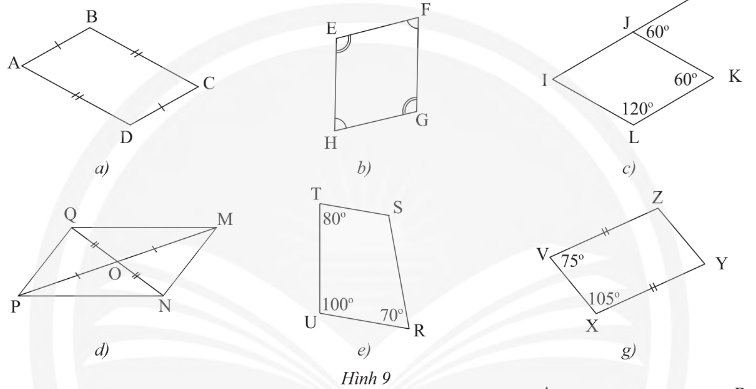


a) Xét tứ giác \(ABCD\) ta có:
\(AB = CD\) (gt)
\(AD = BC\) (gt)
Suy ra: \(ABCD\) là hình bình hành
b) Xét tứ giác \(EFGH\) ta có:
\(\widehat {\rm{E}} = \widehat G\) (gt)
\(\widehat F = \widehat H\) (gt)
Suy ra \(EFGH\) là hình bình hành
c) Ta có: \(\widehat J = \widehat {\rm{K}} = 60^\circ \) (gt)
Mà hai góc ở vị trí so le trong
Suy ra \(IJ\) // \(KL\) (1)
Ta có: \(\widehat K + \widehat L = 60^\circ + 120^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra \(JK\;{\rm{//}}\;IL\) (2)
Từ (1), (2) suy ra \(IJKL\) là hình bình hành
d) Xét tứ giác \(MNPQ\) ta có:
\(O\) là trung điểm của \(NQ\) (do \(OQ = ON\))
\(O\) là trung điểm của \(MP\) (do \(OP = OM\))
Suy ra \(MNPQ\) là hình bình hành
e) Tứ giác \(TSRU\) không là hình bình hành
g) Ta có: \(\widehat {\rm{V}} + \widehat {\rm{X}} = 75^\circ + 105^\circ = 180^\circ \)
Mà hai góc ở vị trí trong cùng phía
Suy ra: \(VZ\) // \(XY\)
Xét tứ giác \(VZYX\) ta có:
\(VZ\) // \(XY\) (cmt)
\(VZ = XY\) (gt)
Suy ra \(VZYX\) là hình bình hành