

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



∆ABC và ∆ABD có:
∠CAB = ∠DAB(gt)
AB là cạnh chung.
∠CBA = ∠DBA (gt)
Nên ∆ABC=∆ABD(g.c.g)
Ta có:
∠ABC + ∠ABD =1800 (Hai góc kề bù).
∠ACB + ∠ACE =1800
Mà ∠ABC = ∠ACB(gt)
Nên ∠ABD = ∠ACE
* ∆ABD và ∆ACE có:
∠ABD = ∠ACE (cmt)
BD=EC(gt)
∠ADB = ∠AEC (gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
∠ADC = ∠AEB (gt)
∠ACD = ∠ABE (gt)
Ta có: DC = DB + BC
EB = EC + BC
Mà BD = EC (gt)
⇒ DC = EB
Nên ∆ADC=∆AEB(g.c.g)

- Hình 116
Ta có ΔABD cân vì AB = AD
ΔACE cân vì AC = AE
Do AB = AD , BC = DE nên AB + BC = AD + DE hay AC = AE
⇒ ΔACE cân
- Hình 117
Ta tính được
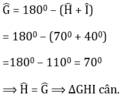
- Hình 118
* ΔOMN là tam giác đều vì ba cạnh bằng nhau OM = MN = NO
* ΔOMK cân tại M vì OM = MK
* ΔONP là tam giác cân tại N vì ON = NP


\(\widehat{A}\)=600, \(\widehat{H}\)=700, \(\widehat{E}\)=400
\(\widehat{L}\)=700, \(\widehat{RNQ}\)=800, \(\widehat{NRP}\)=800

Hình 68.
Xét \(\Delta ABC;\Delta ABD\):
AC = AD (gt)
AB chung
BC = BD (gt)
=> \(\Delta ABC=\Delta ABD\left(c.c.c\right)\)
Hình 69.
Xét \(\Delta MNQ;\Delta QPM:\)
MN = QP (gt)
MQ chung
NQ = PM (gt)
=> \(\Delta MNQ=\Delta QPM\left(c.c.c\right)\)
Hình 70. Gọi giao điểm của HK và EI là O.
Xét tg HEI; tg KIE:
EH = KI
EI chung
HI = KE
=> tg HEI = tg KIE (c.c.c)
=> g HEI = g KIE hay g HEO = g OIK
Tương tự: tg HIK = tg KEH (c.c.c)
=> g IHK = g EKH hay g IHO = g OKE
Xét tg HEO; tg KIO:
g HEO = g OIK (c/m trên)
HE = KI
g EHO = g OKI (cộng góc)
=> tg HEO = tg KIO (g.c.g)
Tương tự: tg HIO = tg KEO (g.c.g)

Giải:
Hình 82.
∆ADB và ∆ADE có:
AB=AE(gt)
\(\widehat{A_1}=\widehat{A_2}\)
AD chung.
Nên ∆ADB = ∆ADE(c.g.c)
Hình 83.
∆HGK và ∆IKG có:
HG=IK (gt)
\(\widehat{G}=\widehat{K}\) (gt)
GK là cạnh chung(gt)
Nên ∆HGK = ∆IKG( c.g.c)
Hình 84.
∆PMQ và ∆PMN có:
MP cạnh chung
\(\widehat{M_1}=\widehat{M_2}\)
Nhưng MN không bằng MQ. Nên \(\Delta\)PMQ không bằng \(\Delta\)PMN.
- Hình 82
Xét ΔADB và ΔADE có:
AB = AE (gt)
AD cạnh chung
Nên ΔADB = ΔADE (c.g.c)
Vậy ΔADB = ΔADE- Hình 83
Xét ΔHGK và ΔIKG có:
HG = IK (gt)
GK cạnh chung
Nên ΔHGK = ΔIKG
Vậy ΔHGK = ΔIKG
- Hình 84
Xét ΔPMQ và ΔPMN có:
PM cạnh chung
Nhưng MN không bằng MQ
Nên ΔPMQ không bằng ΔPMN
Vậy ΔPMQ không bằng ΔPMN

Xét tam giác ABC trên hình vẽ ta có:
AB = AC = 6 ô vuông (với điều kiện tất cả ô vuông đều bằng nhau).
=> Tam giác ABC là tam giác cân và cân tại A.


Tam giác ABC có AB = AC (theo đề bài)
Suy ra: tam giác ABC cân tại A( dựa theo định nghĩa tam giác cân)
=> góc ABC = góc ACB ( dựa theo tính chất tam giác cân)
=> góc ABC = góc ACB = \(\left(180^0-36^0\right):2=72^0\)
Có góc ACB + góc ACE = \(180^0\) (2 góc kề bù)
=> góc ACE = \(180^0\)- góc ACB
=> góc ACE = \(180^0-72^0=108^0\)
Tam giác ACE có góc CAE + góc CEA + góc ACE = \(180^0\)(tổng 3 góc của 1 tam giác)
=> góc CEA = \(180^0-\left(108^0+36^0\right)=36^0\)(*)
Tam giác ADE có góc BDA = góc CEA = \(36^0\)
=> tam giác ADE cân tại A ( dựa theo tính chất của tam giác cân)