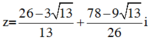Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Phương pháp:
Từ ![]() tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
tìm ra quỹ tích điểm M(x;y) biểu diễn cho số phức z=x+yi
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất
nhỏ nhất
![]()
Cách giải: Gọi z=x+ui ta có:
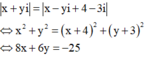
Gọi điểm M(x;y) là điểm biểu diễn cho số phức z và A(-1;1) ;B(2;-3) ta có:
![]() nhỏ nhất.
nhỏ nhất.
Ta có: ![]()
Dấu bằng xảy ra ![]()
![]() M thuộc trung trực của AB.
M thuộc trung trực của AB.
Gọi I là trung điểm của AB ta có ![]()
Phương trình đường trung trực của AB là
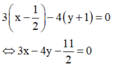
Để ![]()
![]() Tọa độ điểm M là nghiệm của hệ phương trình
Tọa độ điểm M là nghiệm của hệ phương trình


Chọn B.
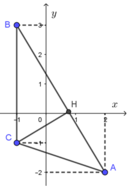
Gọi M (x; y) là điểm biểu diễn của số phức z trên mặt phẳng Oxy.
Gọi điểm A(2; -2) ; B(-1; 3) và C(-1; -1)
Phương trình đường thẳng AB: 5x + 3y - 4 = 0.
Khi đó theo đề bài ![]()
Ta có ![]() . Do đó quỹ tích M là đoạn thẳng AB.
. Do đó quỹ tích M là đoạn thẳng AB.
Tính CB = 4 và ![]() .
.
Hình chiếu H của C trên đường thẳng AB nằm trên đoạn AB.
Vậy 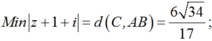
![]()

Đáp án D
Phương pháp:
- Biểu diễn số phức và giải bài toán tìm GTLN trên mặt phẳng tọa độ.
Cách giải: Gọi I(1;1), J(-1;-3), A(2;3).
Xét số phức ![]() , có điểm biểu diễn là M(x;y)
, có điểm biểu diễn là M(x;y)
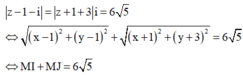
![]() M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
M di chuyển trên đường elip có tiêu điểm I và J, độ dài trục lớn là
3
5
Tìm giá trị lớn nhất của ![]() tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
tức là tìm độ dài lớn nhất của đoạn AM khi M di chuyển trên elip.
Ta có:
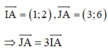
điểm A nằm trên trục lớn của elip.
![]() AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
AM đạt độ dài lớn nhất khi và chỉ khi M trùng với B, là đỉnh của elip nằm trên trục lớn và khác phía A so với điểm I.
Gọi S là trung điểm của IJ
![]() S(0;-1)
S(0;-1)
Độ dài đoạn AB=SA+SB
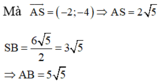
Vậy ![]()
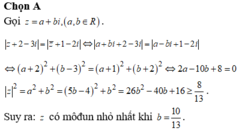
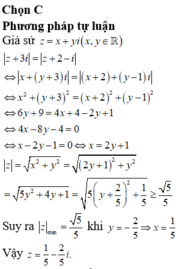

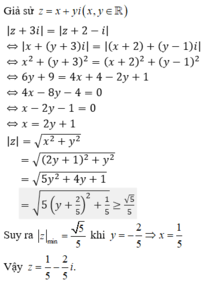
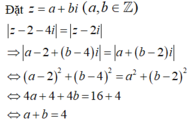
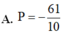
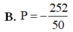
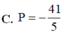
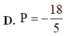





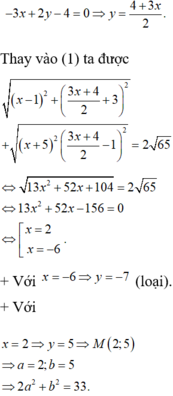
Chọn A.
Đặt z = x+ yi.
Khi đó
Các điểm M biểu diễn số phức z thỏa mãn hệ thức đã cho nằm trên đường tròn tâm I(2;-3) và bán kính R = 3/2.
Ta có: min|z| khi và chỉ khi M nằm trên đường tròn và gần O nhất.
Đó là điểm M1( là giao điểm của tia IO với đường tròn) (Bạn đọc tự vẽ hình).
Ta có: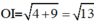 . Kẻ
. Kẻ 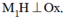
Theo định lý talet ta có:
Vậy