OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
21 tháng 2 2018
Trong các khẳng định sau, số khẳng định đúng là:a) Tập nghiệm của phương trình x 2 + 3 x x = 0  là {0; 3}b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0  là {-2}c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8  là {0} A. 1                       B. 2  ...
Đọc tiếp

Trong các khẳng định sau, số khẳng định đúng là:

a) Tập nghiệm của phương trình x 2 + 3 x x = 0  là {0; 3}

b) Tập nghiệm của phương trình x 2 - 4 x - 2 = 0  là {-2}

c) Tập nghiệm của phương trình x - 8 x - 7 = 1 7 - x + 8  là {0}

A. 1                      

B. 2                      

C. 0                      

D. 3
#Toán lớp 8
1
CM
Cao Minh Tâm
21 tháng 2 2018

Đáp án cần chọn: A

Đúng(0)
QK
Quang Khai
16 tháng 2 2023
Câu 1. trong các phương trình sau, phương trình nào là phương trình bậc nhất 1 ẩn:A. 6x-5=0       B. 3x^2=0        C.  8x-5+2x^2=0          D. x^3+1=0.Câu 2. Nghiệm của phương trình ax+b=0 là:A. x= a/b        B. x=-a/b          C. x= b/a            D. x=-b/a.Câu 3. nghiệm của phương trình 2x-1=3 là :A. x=3         B.x=4          C. x=1         D. x=2.Câu 4. Phương trình 4x-4=2x+a có nghiệm x=-1 khi:A. a=3         B. a=-7         C. a=-6           D. a=-3.Câu 5....
Đọc tiếp

Câu 1. trong các phương trình sau, phương trình nào là phương trình bậc nhất 1 ẩn:

A. 6x-5=0       B. 3x^2=0        C.  8x-5+2x^2=0          D. x^3+1=0.

Câu 2. Nghiệm của phương trình ax+b=0 là:

A. x= a/b        B. x=-a/b          C. x= b/a            D. x=-b/a.

Câu 3. nghiệm của phương trình 2x-1=3 là :

A. x=3         B.x=4          C. x=1         D. x=2.

Câu 4. Phương trình 4x-4=2x+a có nghiệm x=-1 khi:

A. a=3         B. a=-7         C. a=-6           D. a=-3.

Câu 5. Nghiệm của phương trình 2x-(3-5x)=11 là:

A. x=3          B.x=1         C. x= -14/3          D.x=2.
#Toán lớp 8
1
NL
Nguyễn Lê Phước Thịnh
16 tháng 2 2023

1A

2D

3D

4C

5D

Đúng(0)
NM
Nguyễn my
19 tháng 3 2023

Trong các phương trình sau phương trình nào là phương trình bậc nhất một ẩn xác định hệ số a,b của phương trình đó 1)0.x-5=0 2)3x²+2=0 3)8x-5=0 4) 3-4x/x=0 5)2x+3=0 6)3/x -5=0
#Toán lớp 8
1
乇尺尺のﾚ
19 tháng 3 2023

phương trình bậc nhất 1 ẩn:

3)8x-5=0(a=8;b=-5)

5)2x+3=0(a=2;b=3)

 

Đúng(2)
乇尺尺のﾚ
19 tháng 3 2023

mấy cái phân số mình ko chắc

 

Đúng(1)
PT
Pham Trong Bach
16 tháng 2 2019

Trong các số -2; -1,5; -1; 0,5; 2/3 ;2 ;3 số nào là nghiệm của mỗi phương trình sau:  3 x - 4 2 + 1 = 0

#Toán lớp 8
1
CM
Cao Minh Tâm
16 tháng 2 2019

Với mỗi phương trình tính giá trị hai vế khi ẩn lần lượt các giá trị -2; -1,5; -1; 0,5; 2/3 ; 2; 3 những giá trị của ẩn mà hai vế phương trình có giá trị bằng nhau là nghiệm của phương trình.

3 x - 4 2  + 1 = 0

x -2 -1,5 -1 0,5 2/3 2 3
3 x - 4 2  + 1 -4 -3,25 -2,5 -0,25 0 2 3,5

Vậy x = 2/3 là nghiệm của phương trình.

Đúng(0)
NT
Nguyễn Thu Giang
23 tháng 1 2020 - olm

trong các số sau -2; -1; 0; 0,5; 3 hãy tìm xem số nào là nghiệm của phương trình x^2-2x=3
#Toán lớp 8
0
PT
Pham Trong Bach
8 tháng 6 2017

Số nào trong các số sau là nghiệm của phương trình 3x +7 = 1 + 2x .

A. -1. 

B. 2 

C. - 6 

D. 6. 
#Toán lớp 8
1
CM
Cao Minh Tâm
8 tháng 6 2017

Đáp án: C

Hướng dẫn giải:

Thay lần lượt các giá trị của x vào 2 vế của phương trình đã cho ta được

(A) Với x = -1 ; VT = 3.(-1) + 7= 4 ; VP = 1 + 2.(-1) = -1 ⇒ VT ≠ VP

(B) Với x = 2 ; VT = 3.2 + 7 = 13 ; VP = 1 + 2.2 = 5 ⇒ VT ≠ VP

(C) Với x = -6 ; VT = 3.(-6) + 7 = -11 ; VP = 1 + 2.(-6) = -11 ⇒ VT = VP

(D) Với x = 6 ; VT = 3.6 + 7 = 25 ; VP = 1 + 2.6 = 13 ⇒ VT ≠ VP

Vậy giá trị x = -6 là nghiệm của phương trình đã cho.

Đúng(0)
SS
Sến Sến
5 tháng 6 2021

Số nào dưới đây là nghiệm chung của hai phương trình x2+12=8x và x2-10x+12=0 ? 

A. −5.  B. 2.  C. 6.  D. 4.  

Các bạn rồi ghi đáp án nhé !! Giups mình bucminh

 
#Toán lớp 8
3
Y
Yeutoanhoc
5 tháng 6 2021

`x^2+12=8x`

`<=>x^2-8x+12=0`

`<=>(x-2)(x-6)=0`

`<=>` $\left[ \begin{array}{l}x=2\\x=6\end{array} \right.$

`x^2-10x+12=0`

`<=>(x-5)^2-13=0`

`<=>` $\left[ \begin{array}{l}x=-\sqrt{13}+5\\x=\sqrt{13}+5\end{array} \right.$

Vậy không cso đáp án do đề sai

Đúng(1)
S
💢Sosuke💢
5 tháng 6 2021

Số nào dưới đây là nghiệm chung của hai phương trình \(x^2+12=8x\) và \(x^2-10x+12=0\) ? 

Giải thích: 

\(\left(1\right)x^2+12=8x\Leftrightarrow x^2-8x+12=0\)

\(\left(2\right)x^2-10x+12=0\)

Nghiệm của phương trình (1) là: \(\left\{{}\begin{matrix}x_1=6\\x_2=2\end{matrix}\right.\)

Nghiệm của phương trình (2) là: ​​\(\left\{{}\begin{matrix}x_1=5+\sqrt{13}\\x_2=5-\sqrt{13}\end{matrix}\right.\)

\(\Rightarrow\) Không có nghiệm chung.​​

Đúng(1)
PT
Pham Trong Bach
27 tháng 10 2018

Số nào trong các số sau là nghiệm của phương trình - 3x - 5 = 2(x - 1)

A. 1

B. -1

C.  - 3 5  

D.  3 5  
#Toán lớp 8
1
CM
Cao Minh Tâm
27 tháng 10 2018

Đáp án: C

Hướng dẫn giải:

Thay lần lượt các giá trị của x vào 2 vế của phương trình đã cho ta được

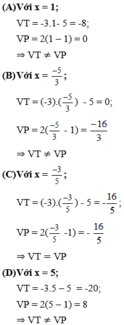
Cách chứng minh một số là nghiệm của một phương trình cực hay, có đáp án | Toán lớp 8

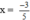Vậy Cách chứng minh một số là nghiệm của một phương trình cực hay, có đáp án | Toán lớp 8 là nghiệm của phương trình đã cho.

Đúng(0)
PB
Preet Baquania
7 tháng 4 2018 - olm

Cho phương trình: \(x^2\) – 3x – 4 = 0

Trong các số - 1; 1; -4; 4, số nào là nghiệm của phương trình?
#Toán lớp 8
3
ND
Nguyễn Đặng Linh Nhi
7 tháng 4 2018

Thay x = -1 vào vế trái của phương trình, ta có:

\(\left(-1\right)^2\) – 3(-1) – 4 = 1 + 3 – 4 = 0

Vậy x = -1 là một nghiệm của phương trình

Tương tự: x = 4 cũng là nghiệm của phương trình

x = 1; x = -4 không phải là nghiệm của phương trình.

Đúng(0)
D
Despacito
7 tháng 4 2018

\(x^2-3x-4=0\)

\(x^2-4x+x-4=0\)

\(x\left(x-4\right)+\left(x-4\right)=0\)

\(\left(x+1\right)\left(x-4\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x=-1\\x=4\end{cases}}\)

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP