Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Trong các số trên, số 0,010010001.... là số vô tỉ.
Vậy đáp án đúng trong câu trên là câu D.
Ta viết các phân số dưới dạng phân số tối giản:
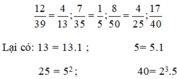
Suy ra: phân số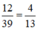 
viết được số thập phân vô hạn tuần hoàn.
Chọn (A). 12/39
Bài 1: Cho 1 ví dụ để bác bỏ các ý kiến sau:
a) Tổng của 2 số vô tỉ là 1 số vô tỉ
Ý kiến: Tổng của hai số vô tỉ luôn là số vô tỉ.
Bác bỏ: Tổng của hai số vô tỉ có thể là một số hữu tỉ.
Ví dụ: Chọn \(x = \sqrt{2}\) và \(y = - \sqrt{2}\).
Tổng của chúng là:
\(x + y = \sqrt{2} + \left(\right. - \sqrt{2} \left.\right) = 0\)
Vì 0 là một số hữu tỉ, nên tổng của hai số vô tỉ này là một số hữu tỉ. Điều này bác bỏ ý kiến rằng tổng của hai số vô tỉ luôn là vô tỉ.
b) Hiệu của 2 số vô tỉ là 1 số vô tỉ
Ý kiến: Hiệu của hai số vô tỉ luôn là số vô tỉ.
Bác bỏ: Hiệu của hai số vô tỉ có thể là một số hữu tỉ.
Ví dụ: Chọn \(x = \sqrt{2}\) và \(y = \sqrt{2}\).
Hiệu của chúng là:
\(x - y = \sqrt{2} - \sqrt{2} = 0\)
Vì 0 là một số hữu tỉ, nên hiệu của hai số vô tỉ này là một số hữu tỉ. Điều này bác bỏ ý kiến rằng hiệu của hai số vô tỉ luôn là vô tỉ.
c) Tích của 2 số vô tỉ là 1 số vô tỉ
Ý kiến: Tích của hai số vô tỉ luôn là vô tỉ.
Bác bỏ: Tích của hai số vô tỉ có thể là một số hữu tỉ.
Ví dụ: Chọn \(x = \sqrt{2}\) và \(y = \frac{1}{\sqrt{2}}\).
Tích của chúng là:
\(x \cdot y = \sqrt{2} \cdot \frac{1}{\sqrt{2}} = 1\)
Vì 1 là một số hữu tỉ, nên tích của hai số vô tỉ này là một số hữu tỉ. Điều này bác bỏ ý kiến rằng tích của hai số vô tỉ luôn là vô tỉ.
d) Thương của 2 số vô tỉ là 1 số vô tỉ
Ý kiến: Thương của hai số vô tỉ luôn là vô tỉ.
Bác bỏ: Thương của hai số vô tỉ có thể là một số hữu tỉ.
Ví dụ: Chọn \(x = \sqrt{2}\) và \(y = \sqrt{2}\).
Thương của chúng là:
\(\frac{x}{y} = \frac{\sqrt{2}}{\sqrt{2}} = 1\)
Vì 1 là một số hữu tỉ, nên thương của hai số vô tỉ này là một số hữu tỉ. Điều này bác bỏ ý kiến rằng thương của hai số vô tỉ luôn là vô tỉ.
Bài 2: Tìm \(x\), \(y\), \(z\)
a) Giải phương trình:
\(\mid x + \frac{19}{5} \mid + \mid y + \frac{1890}{1975} \mid + \mid z - 2023 \mid = 0\)
Để tổng của ba giá trị tuyệt đối bằng 0, mỗi giá trị trong các dấu giá trị tuyệt đối phải bằng 0. Do đó, ta có:
\(x + \frac{19}{5} = 0 , y + \frac{1890}{1975} = 0 , z - 2023 = 0\)
Giải các phương trình trên:
- \(x = - \frac{19}{5}\)
- \(y = - \frac{1890}{1975}\)
- \(z = 2023\)
Vậy:
\(x = - \frac{19}{5} , y = - \frac{1890}{1975} , z = 2023\)
b) Giải phương trình:
\(\mid x - \frac{9}{2} \mid + \mid y + \frac{4}{3} \mid + \mid z + \frac{7}{2} \mid \leq 0\)
Tổng của ba giá trị tuyệt đối không thể nhỏ hơn 0, và tổng này chỉ bằng 0 khi mỗi giá trị tuyệt đối đều bằng 0. Vì vậy, ta có:
\(x - \frac{9}{2} = 0 , y + \frac{4}{3} = 0 , z + \frac{7}{2} = 0\)
Giải các phương trình trên:
- \(x = \frac{9}{2}\)
- \(y = - \frac{4}{3}\)
- \(z = - \frac{7}{2}\)
Vậy:
\(x = \frac{9}{2} , y = - \frac{4}{3} , z = - \frac{7}{2}\)
Bài 3: Tìm giá trị nhỏ nhất của các biểu thức
a) Tìm giá trị nhỏ nhất của biểu thức:
\(A = \mid 2 x - \frac{1}{3} \mid + 107\)
Biểu thức \(A\) có giá trị nhỏ nhất khi \(\mid 2 x - \frac{1}{3} \mid = 0\), tức là \(2 x = \frac{1}{3}\), hoặc \(x = \frac{1}{6}\).
Khi \(x = \frac{1}{6}\), ta có:
\(A = 0 + 107 = 107\)
Vậy giá trị nhỏ nhất của \(A\) là 107.
b) Tìm giá trị nhỏ nhất của biểu thức:
\(B = \mid x + \frac{1}{2} \mid + \mid x + \frac{1}{3} \mid + \mid x + \frac{1}{4} \mid\)
Để giá trị của \(B\) nhỏ nhất, ta cần chọn giá trị của \(x\) sao cho các giá trị tuyệt đối trong biểu thức nhỏ nhất. Các điểm mà các giá trị tuyệt đối bằng 0 là:
\(x = - \frac{1}{2} , x = - \frac{1}{3} , x = - \frac{1}{4}\)
Do đó, ta chọn giá trị \(x = - \frac{1}{3}\) vì nó nằm giữa các giá trị trên, giúp các giá trị tuyệt đối đạt giá trị nhỏ nhất. Khi \(x = - \frac{1}{3}\), ta có:
\(B = \mid - \frac{1}{3} + \frac{1}{2} \mid + \mid - \frac{1}{3} + \frac{1}{3} \mid + \mid - \frac{1}{3} + \frac{1}{4} \mid\)
Tính các giá trị:
\(B = \mid - \frac{1}{3} + \frac{1}{2} \mid + 0 + \mid - \frac{1}{3} + \frac{1}{4} \mid\)\(B = \mid - \frac{2}{6} + \frac{3}{6} \mid + 0 + \mid - \frac{4}{12} + \frac{3}{12} \mid\)\(B = \frac{1}{6} + 0 + \frac{1}{12} = \frac{2}{12} + \frac{1}{12} = \frac{3}{12} = \frac{1}{4}\)
Vậy giá trị nhỏ nhất của \(B\) là \(\frac{1}{4}\).
Cho \(x\) là số hữu tỉ khác \(0\), \(y\) là số vô tỉ.
- Chứng minh \(x + y\) vô tỉ.
Giả sử \(x + y\) hữu tỉ. Khi đó
\(y = \left(\right. x + y \left.\right) - x .\)
Vì “hữu tỉ trừ hữu tỉ = hữu tỉ”, suy ra \(y\) hữu tỉ — mâu thuẫn với giả thiết \(y\) vô tỉ.
Vậy \(x + y\) là số vô tỉ.
- Chứng minh \(x y\) vô tỉ.
Giả sử \(x y\) hữu tỉ. Do \(x \neq 0\), ta có
\(y = \frac{x y}{x} .\)
Vì “hữu tỉ chia hữu tỉ khác 0 = hữu tỉ”, suy ra \(y\) hữu tỉ — mâu thuẫn.
Vậy \(x y\) là số vô tỉ.
mik chỉ biết bài 1,bn thông cảm nha! có gì cho mình xin 1 tick với nhé!
Số hữu tỉ dương: \(\frac{-3}{-5};\frac{2}{3}\)
Số hữu tỉ âm: \(\frac{-3}{7};\frac{1}{-5}\)
Số không phải là số hữu tỉ âm mà cũng không phải là số hữu tỉ âm: \(\frac{0}{-2}\)
8a=5b
26c=15b
vì 8a=5b
24a=15b=26c
tỉ số của a và c là: 12/13
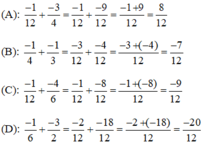
Chọn (D) 0,010010001...