Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
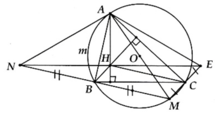
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3
Đáp án A
Vì tứ giác ABCD là hình bình hành và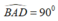 
nên ABCD là hình chữ nhật.
Gọi O là giao điểm hai đường chéo.
Theo tính chất hình chữ nhật ta có:
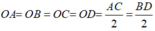
Do đó, O là tâm đường tròn ngoại tiếp hình chữ nhật ABCD.
Xét hình bình hành ABCD ngoại tiếp (O)
Theo đầu bài ta suy ra các cạnh của hình bình hành là tiếp tuyến của (O)
Gọi M , N , P , Q là các tiếp điểm của đường tròn với các cạnh như hình vẽ
Theo tính chất tiếp tuyến có: CM = CN ; AP = AQ ; BM = BQ ; PD = DN
=> CM + BM + AP + PD = CN + DN + AQ + BQ
=> 2BC = 2AB
=> BC = AB
Kẻ AH \(\perp\)BC ta có: AB > AH (Đường xiên , hình chiếu)
Dấu "=" xảy ra khi ^ABC = 90o
Ta có : OM ⊥ BC ; OP ⊥ AD , AD // BC
=> P , O , M thẳng hàng
Do đó AH = PM = 2r
\(S_{ABCD}=AH.BC=2r.AB\ge2r.AH=2r.2r=4r^2\)
Dấu "=" xảy ra \(\Leftrightarrow AH\equiv AB\Leftrightarrow\widehat{ABC}=90^o\)
Mà ABCD là hình bình hành
=> ABCD là hình vuông
Vậy trong các hình bình hành ngoại tiếp đường tròn (O;r) thì hình vuông có diện tích nhỏ nhất và bằng 4r2
hình đâu bn
ko có hình sao biết đc!!