Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án đúng là D
+ Xét điểm \(\left( {1;1} \right)\) ta có: \(y = 2 - 4.1 = - 2 \ne 1\). Do đó, điểm \(\left( {1;1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {2;0} \right)\) ta có: \(y = 2 - 4.2 = - 6 \ne 2\). Do đó, điểm \(\left( {2;0} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {1; - 1} \right)\) ta có: \(y = 2 - 4.1 = - 2 \ne - 1\). Do đó, điểm \(\left( {1; - 1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {1; - 2} \right)\) ta có: \(y = 2 - 4.1 = - 2\). Do đó, điểm \(\left( {1; - 2} \right)\) thuộc đồ thị hàm số.

Xét điểm \(M\left( { - 1; - 4} \right)\) ta có:
\(f\left( { - 1} \right) = 4.\left( { - 1} \right) = - 4\). Do đó, điểm \(M\left( { - 1; - 4} \right)\) thuộc vào đồ thị hàm số \(y = 4x\).
Xét điểm \(N\left( {1; - 4} \right)\) ta có:
\(f\left( 1 \right) = 4.1 = 4 \ne - 4\). Do đó, điểm \(N\left( {1; - 4} \right)\) không thuộc vào đồ thị hàm số \(y = 4x\).
Xét điểm \(P\left( {\dfrac{1}{4};1} \right)\) ta có:
\(f\left( {\dfrac{1}{4}} \right) = 4.\dfrac{1}{4} = 1\). Do đó, điểm \(P\left( {\dfrac{1}{4};1} \right)\) không thuộc vào đồ thị hàm số \(y = 4x\).

\(A\left( { - 2;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(A\) là –2 và tung độ của điểm \(A\) là 0.
\(B\left( {0;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(B\) là 0 và tung độ của điểm \(B\) là 4.
\(C\left( {5;4} \right)\) \( \Rightarrow \) hoành độ của điểm \(C\) là 5 và tung độ của điểm \(C\) là 4.
\(D\left( {3;0} \right)\) \( \Rightarrow \) hoành độ của điểm \(D\) là 3 và tung độ của điểm \(D\) là 0.
Biểu diễn các điểm \(A;B;C;D\) trên mặt phẳng tọa độ ta được:
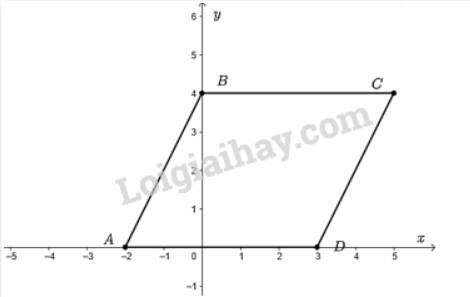
Vì hai điểm \(B;C\) có tung độ bằng nhau nên \(BC\) song song với \(Ox\); Hai điểm \(A;D\) có tung độ bằng nhau nên \(AD\) song song với \(Ox\).
Do đó, \(BC//AD\).
Lại có, \(AD = \left| {3 - \left( { - 1} \right)} \right| = 4;BC = \left| {4 - 0} \right| = 4\). Do đó, \(AD = BC\).
Xét tứ giác \(ABCD\)có:
\(AD = BC\)
\(BC//AD\)
Do đó, tứ giác \(ABCD\) là hình bình hành.

Baif2:
A=\(12x^2+20x-8+9\)
=\(4\left(3x^2+5x-2\right)+9\)
=4.0+9
= 9
vậy A=............
hc tốt
\(3x^2+5x-2=0\)
\(\Leftrightarrow3x^2-x+6x-2=0\)
\(\Leftrightarrow x\left(3x-1\right)+2\left(3x-1\right)=0\)
\(\Leftrightarrow\left(3x-1\right)\left(x+2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-2\\x=\frac{1}{3}\end{cases}}\)

Từ điểm \(y = 2\) trên \(Oy\) vẽ đường thẳng vuông góc với \(Oy\) cắt đồ thị hàm số tại điểm \(C\). Khi đó, điểm \(C\) là điểm trên đồ thị hàm số có tung độ bằng 2.
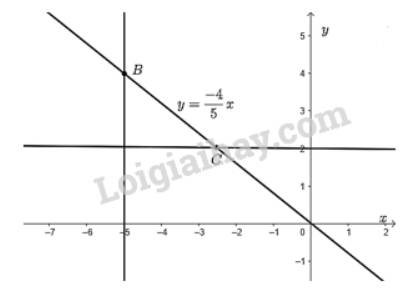

Vẽ đồ thị hàm số \(y = \dfrac{{ - 4}}{5}x\).
Đồ thị hàm số là đường thẳng đi qua hai điểm \(O\) và \(P\).
Từ điểm \(x = - 5\) trên \(Ox\)vẽ đường thẳng vuông góc với \(Ox\) cắt đồ thị hàm số tại điểm \(B\). Khi đó, điểm \(B\) là điểm trên đồ thị hàm số có hoành độ bằng -5.


a) Ta có:
\(f\left( {\dfrac{1}{5}} \right) = \dfrac{5}{{4.\dfrac{1}{5}}} = \dfrac{5}{{\dfrac{4}{5}}} = 5:\dfrac{4}{5} = 5.\dfrac{5}{4} = \dfrac{{25}}{4};\)
\(f\left( { - 5} \right) = \dfrac{5}{{4.\left( { - 5} \right)}} = \dfrac{5}{{ - 20}} = \dfrac{{ - 1}}{4};\)
\(f\left( {\dfrac{4}{5}} \right) = \dfrac{5}{{4.\dfrac{4}{5}}} = \dfrac{5}{{\dfrac{{16}}{5}}} = 5:\dfrac{{16}}{5} = 5.\dfrac{5}{{16}} = \dfrac{{25}}{{16}}\)
b) Ta có:
\(f\left( { - 3} \right) = \dfrac{5}{{4.\left( { - 3} \right)}} = \dfrac{5}{{ - 12}} = \dfrac{{ - 5}}{{12}};\)
\(f\left( { - 2} \right) = \dfrac{5}{{4.\left( { - 2} \right)}} = \dfrac{5}{{ - 8}} = \dfrac{{ - 5}}{8};\)
\(f\left( { - 1} \right) = \dfrac{5}{{4.\left( { - 1} \right)}} = \dfrac{5}{{ - 4}} = \dfrac{{ - 5}}{4};\)
\(f\left( { - \dfrac{1}{2}} \right) = \dfrac{5}{{4.\left( { - \dfrac{1}{2}} \right)}} = \dfrac{5}{{\dfrac{{ - 4}}{2}}} = \dfrac{5}{{ - 2}} = \dfrac{{ - 5}}{2}\);
\(f\left( {\dfrac{1}{4}} \right) = \dfrac{5}{{4.\dfrac{1}{4}}} = \dfrac{5}{{\dfrac{4}{4}}} = \dfrac{5}{1} = 5\);
\(f\left( 1 \right) = \dfrac{5}{{4.1}} = \dfrac{5}{4}\);
\(f\left( 2 \right) = \dfrac{5}{{4.2}} = \dfrac{5}{8}\)
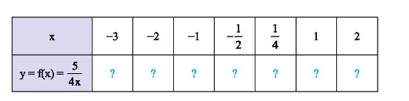
Ta có bảng sau:
\(x\) | –3 | –2 | –1 | \( - \dfrac{1}{2}\) | \(\dfrac{1}{4}\) | 1 | 2 |
\(y = f\left( x \right) = \dfrac{5}{{4x}}\) | \(\dfrac{{ - 5}}{{12}}\) | \(\dfrac{{ - 5}}{8}\) | \(\dfrac{{ - 5}}{4}\) | \(\dfrac{{ - 5}}{2}\) | 5 | \(\dfrac{5}{4}\) | \(\dfrac{5}{8}\) |

\(a,2\left(x-y\right)\left(x+y\right)+\left(x+y\right)^2+\left(x-y\right)^2\)
\(=2x^2+2y^2+x^2+2xy+y^2+x^2-2xy+y^2=3\left(x^2+y^2\right)\)\(b,\left(5x-1\right)+2\left(1-5x\right)\left(4x+5\right)+\left(5x+4\right)\)\(=\left[\left(5x-1\right)-\left(5x+4\right)\right]^2=25\)
c)\(Q=\left(x-y\right)^3+\left(x+y\right)^3+\left(x-y\right)^3-3xy\left(x+y\right)\)
\(=x^3-3x^2y+3xy^2-y^3+x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-3xy^2-3x^2y\)
\(=x^3+y^3\)
d)\(P=12\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(2P=\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(2P=\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(2P=\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(2P=\left(5^{16}-1\right)\left(5^{16}+1\right)\)
\(2P=5^{32}-1\Rightarrow P=\dfrac{5^{32}-1}{2}\)
Đáp án đúng là D
+ Xét điểm \(\left( {1;1} \right)\) ta có: \(y = - 5.1 + 5 = 0 \ne 1\). Do đó, điểm \(\left( {1;1} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {2;0} \right)\) ta có: \(y = - 5.2 + 5 = - 5 \ne 0\). Do đó, điểm \(\left( {2;0} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {0;4} \right)\) ta có: \(y = - 5.0 + 5 = 5 \ne 4\). Do đó, điểm \(\left( {0;4} \right)\)không thuộc đồ thị hàm số.
+ Xét điểm \(\left( {2; - 5} \right)\) ta có: \(y = - 5.2 + 5 = - 5\). Do đó, điểm \(\left( {2; - 5} \right)\) thuộc đồ thị hàm số.