
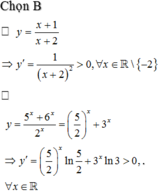

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



y'=1/3*3x^2-2x+3=x^2-2x+3=(x-1)^2+2>0
=>y=1/3x^3-x^2+3x+4 luôn đồng biến trên từng khoảng xác định
\(y=\sqrt{x^2+4}\)
=>\(y'=\dfrac{-\left(x^2+4\right)'}{\left(x^2+4\right)^2}=\dfrac{-\left(2x\right)}{\left(x^2+4\right)^2}\)
=>Hàm số này không đồng biến trên từng khoảng xác định
\(y=x^3+4x-sinx\)
=>y'=3x^2+4-cosx
-1<=-cosx<=1
=>3<=-cosx+4<=5
=>y'>0
=>Hàm số luôn đồng biến trên từng khoảng xác định
y=x^4+x^2+2
=>y'=4x^3+2x=2x(2x^2+1)
=>Hàm số ko đồng biến trên từng khoảng xác định

a) Tập xác định: D = R\{m}
Hàm số đồng biến trên từng khoảng (−∞;m),(m;+∞)(−∞;m),(m;+∞)khi và chỉ khi:
y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2y′=−m2+4(x−m)2>0⇔−m2+4>0⇔m2<4⇔−2<m<2
b) Tập xác định: D = R\{m}
Hàm số nghịch biến trên từng khoảng khi và chỉ khi:
y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0y′=−m2+5m−4(x+m)2<0⇔−m2+5m−4<0
[m<1m>4[m<1m>4
c) Tập xác định: D = R
Hàm số nghịch biến trên R khi và chỉ khi:
y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3y′=−3x2+2mx−3≤0⇔′=m2−9≤0⇔m2≤9⇔−3≤m≤3
d) Tập xác định: D = R
Hàm số đồng biến trên R khi và chỉ khi:
y′=3x2−4mx+12≥0⇔′=4m2−36≤0⇔m2≤9⇔−3≤m≤3

3.
\(y'=\dfrac{3m-1}{\left(x+3m\right)^2}\)
Hàm nghịch biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-1< 0\\-3m\le6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m< \dfrac{1}{3}\\m\ge-2\end{matrix}\right.\)
\(\Rightarrow-2\le m< \dfrac{1}{3}\Rightarrow m=\left\{-2;-1;0\right\}\)
4.
\(y'=\dfrac{3m-2}{\left(x+3m\right)^2}\)
Hàm đồng biến trên khoảng đã cho khi:
\(\left\{{}\begin{matrix}3m-2>0\\-3m\ge-6\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m>\dfrac{2}{3}\\m\le2\end{matrix}\right.\)
\(\Rightarrow\dfrac{2}{3}< m\le2\Rightarrow m=\left\{1;2\right\}\)

\(\left(\frac{2x-1}{x+2}\right)'=\frac{5}{\left(x+2\right)^2}>0\)
Vậy hàm số \(y=\frac{2x-1}{x+2}\) đồng biến trên R. Chọn A.
A. là hàm phân thức bậc nhất trên bậc nhất nên không đồng biến trên \(ℝ\).
B., D. là đa thức, có hệ số cao nhất âm nên cũng không thể đồng biến trên \(ℝ\).
C>: \(\left(x^3+2x+1\right)'=3x^2+2>0,\forall x\inℝ\).
Ta chọn C.

1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)